Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 23.Exercício - Ex. 06

Faça o esboço da cônica descrita pela equação dada em cada caso.

  1. x 2 + 2 3 x y + 3 y 2 + 8 3 x - 8 y + 32 = 0 .
  2. x 2 - 2 x y + y 2 - 5 2 x + 3 2 y + 10 = 0 .

Passo 1

  1. Vamos inicialmente eliminar os termos lineares.

    2. Para a cônica em questão, temos a = 1 ,   b = 2 3 ,   c = 3 ,   d = 8 3 ,   e = - 8 ,   f = 32 . Assim,

    M 3 = a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f = 1 3 4 3 3 3 - 4 4 3 - 4 32

    Portanto, temos o seguinte sistema:

    h + 3 k + 4 3 = 0 3 h + 3 k - 4 = 0

    Notemos que, ao multiplicar a primeira equação por 3 , ficamos

    3 h + 3 k + 12 = 0

    Porém, da segunda, vem que 3 h + 3 k = 4 , de modo que

    16 = 0

    o que é falso!!! Logo, o sistema não admite solução. Se o sistema não admite solução, significa que a cônica não possui centro. Assim, ou é uma parábola, ou o conjunto vazio.

    Passo 2

    Vamos, portanto, fazer uma rotação de modo a eliminar os termos quadráticos.

    cot ⁡ 2 θ = 3 - 1 2 3 = 1 3 ⟹ 2 θ = 60 °

    Portanto,

    a ' + c ' = 1 + 3 a ' - c ' = 2 3 sin ⁡ 60 ° ⟹ a ' + c ' = 4 a ' - c ' = 4 ∴ c ' = 0   e   a ' = 4

    Devemos calcular d ' e e ' .

    d ' = d cos ⁡ 30 ° + e sin ⁡ 30 ° = 8 3 3 2 - 8 ⋅ 1 2 = 12 - 4 = 8

    e ' = - d sin ⁡ 30 ° + e cos ⁡ 30 ° = - 8 3 1 2 - 8 ⋅ 3 2 = - 8 3

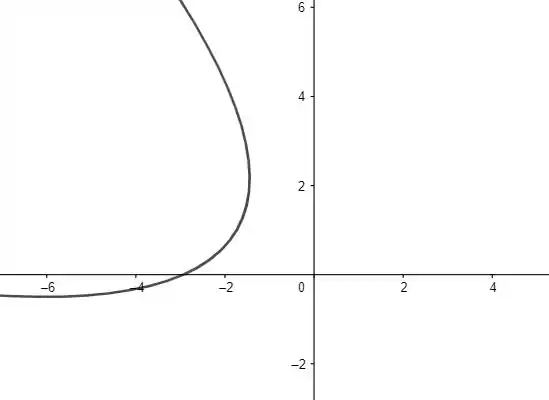
    Portanto, a nova equação da elipse é:

    4 x 2 + 8 x - 8 3 y + 32 = 0 ⟹ 8 3 y = 4 x 2 + 2 x + 1 + 28

    y - 7 3 6 = 3 2 x + 1 2

    Passo 3

  2. Temos a = 1 ,   b = - 2 ,   c = 1 ,   d = - 5 2 ,   e = 3 2 ,   f = 10 .

Montando a matriz:

M 3 = a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f = 1 - 1 - 5 2 2 - 1 1 3 2 2 - 5 2 2 3 2 2 10

Assim, montamos o sistema:

k - h - 5 2 2 = 0 - k + h + 3 2 2 = 0

Porém, novamente vemos que o sistema não possui solução (basta somar as duas equações para verificar isso).

Passo 2

Vamos então rotacionar os eixos:

cot ⁡ 2 θ = c - a b = 1 - 1 - 2 = 0 ⟹ 2 θ = 90 °

Assim,

a ' + c ' = 1 + 1 a ' - c ' = - 2 sin ⁡ 90 ° ⟹ a ' + c ' = 2 a ' - c ' = - 2 ⟹ a ' = 0   e   c ' = 2

Vamos calcular d ' e e ' :

d ' = d cos ⁡ 45 ° + e sin ⁡ 45 ° = - 5 2 ⋅ 1 2 + 3 2 ⋅ 1 2 = - 2

e ' = - d sin ⁡ 45 ° + e cos ⁡ 45 ° = 5 2 ⋅ 1 2 + 3 2 ⋅ 1 2 = 8

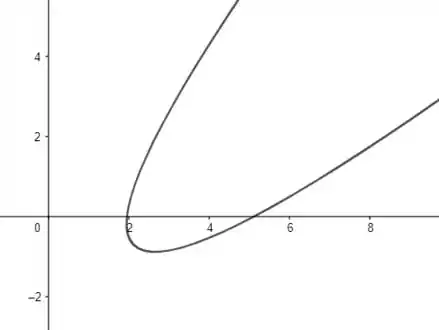
Portanto, a nova equação é:

2 y 2 - 2 x + 8 y + 10 = 0 ⟺ y 2 - x + 4 y + 5 = 0 ⟺

y 2 + 4 y + 4 = x - 1 ⟺ y + 2 2 = x - 1

Notamos que a curva novamente é uma parábola.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada parte, encontre a matriz canônica do operador matricial dado. T:R 2→R 2 projeta cada vetor ortogonalmente sobre o eixo x e, em seguida, reflete esse vetor no eixo y .
Mostre que T( x ,y )=( 0 ,0 ) define um operador matricial em R2, mas T( x ,y )=( 1 ,1 ) não.
Seja T A:R 3→R 3 a multiplicação por. A = - 1 3 0 2 1 2 4 5 - 3 e sejam e 1 , e 2 e e 3 os vetores da base canônica de R 3 . Em cadaparte, encontre o vetor por inspeção. T A ( e 1 ) ,T A e 2 , T A ( e
Prove: uma matriz A de tamanho nxn é invertível se, e só se, o sistema linear A x =w tem exatamente uma solução com qualquer vetor w em R n tal que o sistema seja consistente.
Sejam A uma matriz nxn tal que d e t A =0 e T:R n→R n a multiplicação por A .a) O que pode ser dito sobre a imagem do operador matricial T ? Dê um exemplo que ilustre sua conclusão.b) O que pode ser d