Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 24.Problemas - Ex. 4d
Identifique geometricamente os seguintes conjuntos
Passo 1
Oiiii, gente!
Bom, primeiro vamos dar uma olhadinha na nossa equação, vemos que são utilizadas todas as coordenadas, logo nosso gráfico vai depender da combinação delas.
Resolvendo essa equação, temos:
Logo de cara vemos que a primeira parte da nossa equação trata-se de uma esfera centrada na origem:
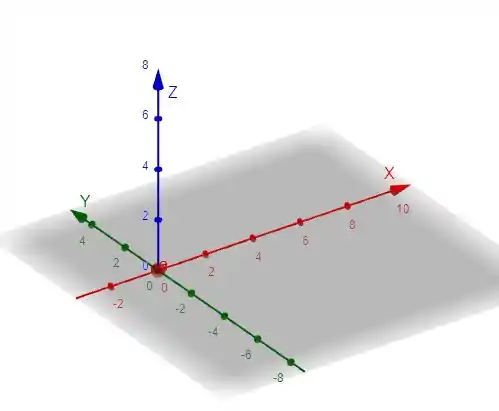
Passo 2
Prosseguindo…
Vamos agora representar a segunda parte da nossa equação que se trata de um plano que contém a reta ( x + y – 1 = 0):
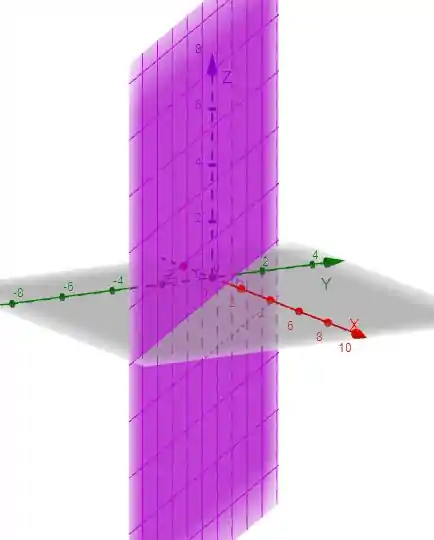
Passo 3
E por fim, juntando essas duas representações temos o gráfico desejado:
Tudo certinho? Bora fazer as outras letrasss!
Bons Estudos!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Escreva uma equação vetorial e equações paramétricas do plano π , utilizando as informações dadas em cada caso.e) π contém os pontos A = 1 ,0 ,2 ,B = - 1 ,1 ,3eC = ( 3 ,- 1 ,1 ) .
Escreva uma equação vetorial e equações paramétricas do plano π , utilizando as informações dadas em cada caso.c) π contém A = ( 1 ,0 ,1 ) e B = ( 0 ,1 ,- 1 ) é paralelo ao segmento de extremidades C
Em uma tarde chuvosa, Cecília resolveu vários exercícios de Geometria Analítica que pediam equações de planos e foi ao final do livro conferir as respostas. Relacionamos a seguir, para cada exercício,
Em uma tarde chuvosa, Cecília resolveu vários exercícios de Geometria Analítica que pediam equações de planos e foi ao final do livro conferir as respostas. Relacionamos a seguir, para cada exercício,
Escreva uma equação vetorial e equações paramétricas do plano π , utilizando as informações dadas em cada caso.d) π contém os pontos A = 1 ,0 ,1 ,B = 2 ,1 ,- 1eC = ( 1 ,- 1 ,0 ) .