Os lados de um triângulo estão sobre as retas y = 2x + 3, y = 2,1·x + 1 e y = 300. Determine se o ponto P = (142, 298) está no interior, no exterior ou num dos lados desse triângulo.

Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??

Desejamos saber qual a posição do ponto P em relação ao triângulo delimitado pelas retas dadas. Visualizando essas retas num gráfico, temos a seguinte região:

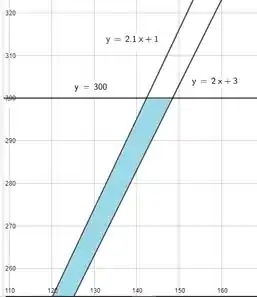
Apesar de não parecer, esta região forma um triângulo. Pois se igualarmos as retas y = 2.1x + 1 e y = 2x + 3, descobrimos que elas se interceptam no ponto (20,43) bem abaixo da reta y = 300.

Com base nisso, vamos definir melhor essa região a partir de desigualdades baseadas em cada uma das retas.

A região é definida abaixo da reta y = 2.1x + 1, acima da reta y = 2x + 3 e abaixo da reta y = 300.

Obtendo assim:

Para saber se o ponto P = (142, 298) está no interior, no exterior ou num dos lados desse triângulo, devemos verificar e o ponto satisfaz todas as desigualdades.

Para , temos que o valor no ponto P é , atendendo a primeira desigualdade.

Para , o ponto P nos dá , atendendo a segunda desigualdade.

Para , temos que em P o valor de y = 298, atendendo a terceira desigualdade.

Logo, podemos dizer que o ponto P é interior ao triângulo.