Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 8
O lado do hexágono regular representado na Figura 11-3 mede . Calcule:
a) b) c)
d) e)
Passo 1
O exercício quer que calculemos a norma dos produtos vetorias. Para isso, temos que lembrar
No item (a), temos
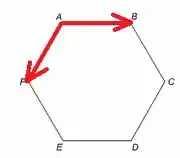
O ângulo entre os vetores é . Assim, como :
Passo 2
Já no item (b), queremos :
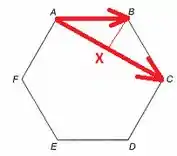
O ângulo entre eles é . Olhando para o triângulo retângulo:
Com isso,
Passo 3
No item (c), temos :
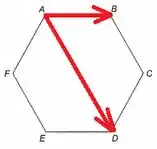
Imaginando o hexágono como vários triângulos equiláteros juntos, temos e . Assim,
Passo 4
No item (d), temos :
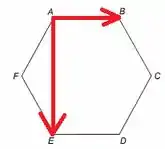
Como os vetores são perpendiculares e
Passo 5
Por fim, no item (e), temos :
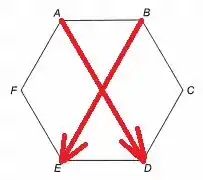
Sabemos que e :
Resposta
Exercícios de Livros Relacionados
Dados a → = ( 3 , - 1,2 ) e b → = 2,3 , 0 , determine um vetor v → tal que v → . a → = - 2 e v → ^ b → = ( 3 , - 2 , - 3 )
Sendo O P → = ( 2,1 , 2 ) e O Q → = 1,1 , 1 , calcule a distância de P à reta O Q , d eQàr e t aO P à e de O à reta P Q .
Sejam O A → = 0,3 , 2 , O B → = 1 , 5 , 1 e O C → = 1 , 2 , - 1 . (a) Demonstre que o quadrilátero de vértices O , A , BeC é um paralelogramo.
Os vetores u → , 1 , 0 , 2 e ( 4,3 , - 1 ) são coplanares. Determine x para que a equação ( 1,0 , 3 ) ^ u → = x , 1,3 tenha solução. Resolva a equação.
Sabemos que u → = a → + b → , v → = a → - b → , a → = 2 , b → = 3 , o ângulo entre a → e b → mede 60 ° , a → = O A → e b → = O B → . Que relação existe entre u → ^ v → e a área do triângulo O A B ? De