Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 32
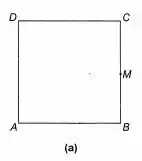
O lado do quadrado da Figura 9-4 (a) mede e é o ponto médio de .
a) Escreva e como combinação linear de e .
b) Calcule a medida angular entre e .
Passo 1
O primeiro passo é escrever e como combinação linear de e . Para isso, note que
Mas note que
Assim,
Da mesma forma,
Passo 2
Por simplicidade, vamos escrever e . Temos que
Queremos achar o ângulo entre e , sendo
Fazendo o produto escalar:
Passo 3
Precisamos também das normas desses vetores:
Portanto,
Assim,
Resposta
Exercícios de Livros Relacionados
Determine a soma dos vetores dados e ilustre geometricamente. - 1 , 0 , 2 , ⟨ 0 , 4 , 0 ⟩
Determine a soma dos vetores dados e ilustre geometricamente. 3 , - 1 , ⟨ - 2,4 ⟩
Determine a soma dos vetores dados e ilustre geometricamente. 0,1 , 2 , ⟨ 0,0 , - 3 ⟩
Determine a , a + b , a - b , 2 a e 3 a + 4 b a = - 3 , - 4 , - 1 , b = 6,2 , - 3
Duas forças F 1 e F 2 com grandezas 10 lb e 12 lb agem sobre um objeto em um ponto P como mostrado na figura. Determine a força resultante F agindo em P assim como sua magnitude, direção e sentido. (I