Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 40
O lado do quadrado mede , é diagonal e é ponto médio de . Calcule .
Passo 1
Vamos começar definindo uma base ortonormal positiva :
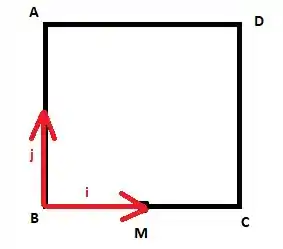
Com essa definição de base, , e .
O vetor é normal ao plano do quadrado e aponta para fora da figura. Beleza?!
Agora temos que escrever e nessa base:
Da mesma forma,
Show de bola?!
Passo 2
Fazendo o produto vetorial:
Assim,
Resposta
Exercícios de Livros Relacionados
Calcule a área do paralelogramo em que três vértices consecutivos são A = (1, 0, 1), B = (2, 1, 3) e C = (3, 2, 4).
Calcule a área do triângulo com vértices A = (1, 2, 1), B = (3, 0, 4) e C = (5, 1, 3).
Sabe-se que o vetor X é ortogonal a i → + j → e a - i → + k → , tem norma 3 e sendo θ o ângulo entre X e j → , tem-se cos θ0. Ache X.
Ache X tal que X × ( i → + k → ) = 2 ( i → + j → - k → ) e X = 6 .
Mostre que os pontos A = (4, 0, 1), B = (5, 1, 3), C = (3, 2, 5), D = (2, 1, 3) são vértices de um paralelogramo. Calcule a sua área.