Verifique se são verdadeiras ou falsas as afirmações seguintes e justifique sua resposta.
a) Se é uma base ortonormal negativa, então
b) Se é uma base ortonormal positiva e e , então
Passo 1
Para o item (a), vamos o regra do reloginho. Como a base é negativa, o produto será positivo no sentido horário:
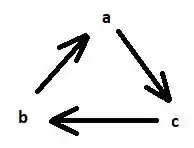
Portanto, fazendo os produtos nesse sentido:
No sentido contrário:
Portanto, a afirmativa é verdadeira.
Passo 2
No item (b) a afirmativa é falsa pois não sabemos que são os vetores , e , conhecemos apenas os vetores da base , que é positiva. A afirmação estaria correta se fosse escrita como