Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.3 - Ex. 11

Se u é um vetor unitário, determine u . v e u . w

Passo 1

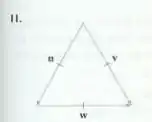
Usando a fórmula do produto escalar esse problema fica simples, já que estamos tratando de um triângulo equilátero, então conhecemos seus lados e ângulos:

u . v = |u| |v| cos theta

|u| = |v| = 1

theta = (pi)/(3)

u . v = 1.1 . cos (pi)/(3)

u . v = (1)/(2)

u . w = |u| |w| cos theta

|u| = |w| = 1

theta = (2 pi)/(3)

O ângulo é 2 pi // 3 pois o ângulo entre os vetores é calculado onde as bases dos dois se tocam. Se movermos vec u para que sua base esteja na base de vec w , vemos que theta = 2 pi // 3

u . w = 1.1 cos (2 pi)/(3)

u . w = - (1)/(2)

Resposta

11. u . v = (1)/(2) , u . w = - (1)/(2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o ângulo entre os vetores. (Estabeleça inicialmente uma expressão exata e depois aproxime o valor até o grau mais próximo.) a = 6 , - 3 , 2 , b = 2 , 1 , - 2
Determine a intensidade do torque em P se for aplicada uma força de 36 lb, como mostrado.
Determine o produto vetorial a × b e verifique que ele é ortogonal a a e b . a = 3 i + 2 j + 4 k , b = i - 2 j - 3 k
Determine o produto vetorial a × b e verifique que ele é ortogonal a a e b . a = 2 i + j - k , b = j + 2 k
Ache um vetor ortogonal ao plano que passa pelos pontos P, Q e R e b) calcule a área do triângulo PQR. P 2,0 , - 3 Q 3,1 , 0 R 5,2 , 2