Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.3 - Ex. 12

Se u é um vetor unitário, determine u . v e u . w

Passo 1

Usando a fórmula do produto escalar esse problema fica simples, basta substituirmos os dados na fórmula:

u . v = |u| |v| cos theta

|u| = 1

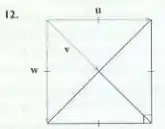
Lembre que a diagonal de um quadrado é l sqrt(2) , como v é a metade de uma diagonal, então v = (sqrt(2))/(2) .

|v| = (sqrt(2))/(2)

theta = (pi)/(4)

u . v = 1 . (sqrt(2))/(2) . cos (pi)/(4)

u . v = (sqrt(2))/(2) ((sqrt(2))/(2)) = (1)/(2)

u . w = |u| |w| cos theta

|u| = |w| = 1

theta = (pi)/(2)

u . w = 1.1 cos (pi)/(2)

u . w = 0

Resposta

12. u . v = (1)/(2) , u . w = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a ⋅ b . a = 12 , b = 15 ,oâ n g u l oe n t r eaebéπ / 6 â é
Determine o vetor projeção e a projeção escalar de b sobre a a = - 1 , - 2,2 , b = 3,3 , 4
Determine o ângulo entre os vetores. (Estabeleça inicialmente uma expressão exata e depois aproxime o valor até o grau mais próximo.) a = 3 , 4 , b = 5 , 12
Determine o vetor projeção e a projeção escalar de b sobre a a = 4 , 2 , 0 , b = 1 , 1 , 1
Determine o vetor projeção e a projeção escalar de b sobre a a = i + k , b = i - j