Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 3.2 - Ex. 21

Mostre que o angulo inscrito em uma semicircunferência é reto.

Passo 1

Fala aeeeee, galera. Tudo bem?

Seja A B C um triângulo inscrito na semicircunferência:

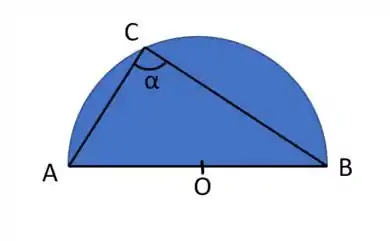
Queremos provar que esse ângulo α é um ângulo reto. Para isso devemos garantir que os vetores A C → e B C → são perpendiculares entre si.

Passo 2

Os vetores A C → e B C → podem ser escritos da seguinte maneira:

B C → = O C → + O B →

A C → = O C → + O A →

Sendo que O A → = - O B → , assim:

A C → = O C → - O B →

Passo 3

Se B C → . B C → = 0 , então α = 90 °

B C → . B C → = 0

O C → + O B → O C → + O A → = 0

O C → 2 - O C → O B → + O C → O B → - O B → 2 = 0

O C → 2 - O B → 2 = 0

Como O C → e O B → são equivalentes ao raio dessa semicircunferência, temos que:

0 = 0

Portanto, α = 90 °

Resposta

D e m o n s t r a ç ã o .

Exercícios de Livros Relacionados

Encontre equações das esferas com centro em ( 2 , - 3,6 ) que toquem (a) o plano x y , (b) o plano y z e (c) o plano x z .
Mostre que a equação representa uma esfera e determine seu centro e raio.15. x 2 + y 2 + z 2 - 6 x + 4 y - 2 z = 11
Descreva em palavras a região de R 3 representada pela equação ou inequação.28. z 2 = 1
Descreva em palavras a região de R 3 representada pela equação ou inequação.25. x3
Determine uma equação da maior esfera com centro em ( 5,4 , 9 ) contida no primeiro octante.