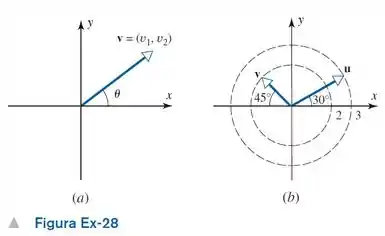
(a) Mostre que os componentes do vetor v na Figura Ex- são e .
(b) Sejam u e v os vetores na Figura Ex-. Use o resultado da parte (a) para encontrar os componentes de uv.
Passo 1
Faaala, galera!! Tudo certo? Vamos resolver esse problema.
Primeiro, supomos que existam os pontos e , como mostra a figura a seguir.
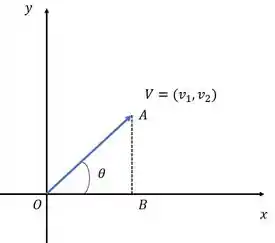
Então
Passo 2
(b) Considerando u temos:
Então
Resposta
(a) Ver passo
(b)