Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 20.Exercício - Ex. 23
As retas , e determinam, com o plano , um tetraedro. Calcule a altura relativa à face situada em , sendo
Passo 1
Primeiro, vamos encontrar as equações vetoriais de cada reta.
Para a reta :
E
Então
Para a reta :
E
Então
Para a reta :
E
Então
Passo 2
O que temos nesse exercício é algo assim:
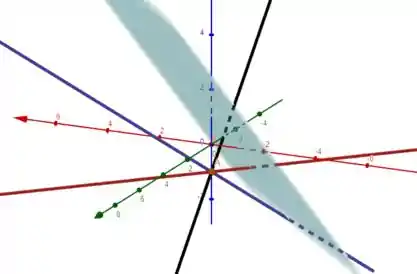
A altura do tetraedro em relação à face é a distância do ponto (laranja) até o plano.
Ta bom, mas qual é o ponto ?? Ele vai ser a intersecção entre as retas. Então, se encontrarmos a intersecção entre e , ou entre e , como você achar melhor hehe teremos o ponto . Aí é só calcular a distância dele até o plano, sabendo que a fórmula de distância entre um ponto e um plano é
Passo 3
Vamos encontrar o ponto , que é a intersecção entre e .
Um ponto genérico de é
E um ponto genérico de , trocando seu parâmetro para , é
Vamos igualar esses dois pontos para encontrar a intersecção:
Igualando as coordenadas, temos
Da última equação, temos que , e das outras duas, temos que , então, .
Substituindo no ponto genérico , temos que a intersecção entre as retas é
Passo 4
Agora é só calcularmos a distância do ponto até o plano para sabermos a altura do tetraedro
Então, a altura do tetraedro em relação à face é :)