Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.2 - Ex. 15
Mostre que se uma reta em ou em não passa pela origem, então ela não é um subespaço. (Sugestão: se ela fosse um subespaço, então…)
Passo 1
Eaew, tudo em cima?
Vamos lembrar a definição de um subespaço, beleza? Se nós temos uma matriz e o conjunto solução do sistema linear homogêneo , em que respeita as seguintes propriedades:
a) Se e pertencem a , então também pertence a .
b) Se pertence a , então também pertence a para todo escalar .
Se temos um subconjunto não vazio que obedece a) e b), então ele é um subespaço do . Belezinha? Isso já é o suficiente para demonstrarmos o que precisamos, bora lá!
Passo 2
Temos que uma reta que não passa pela origem pode ser parametrizada da seguinte maneira:
Para que ela seja um subespaço seria necessário que:
Note que a solução trivial não é interessante, portanto, teremos algo do tipo:
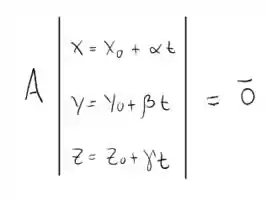
Nós podemos expandir este sistema, note que:
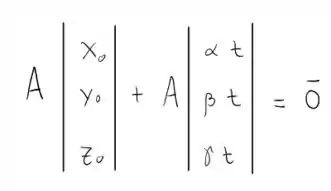
Okay, mas e daí? Vamos dar uma olhada na parametrização de uma reta que passa pela origem! Saca só!
Passo 3
Uma reta que passa na origem tem a seguinte parametrização:
Note que em , a relação é respeitada, esta propriedade no entanto, nos garante que para outros valores de a propriedade ainda tenha validade. Note que se eu somar outro vetor do mesmo tipo (propriedade a) ou multiplicar esse sistema por um escalar (propriedade b), isso continua sendo uma solução. Mas porquê isso é importante? No caso em que temos em a propriedade não é válida, e portanto, a relação do sistema homogêneo não é válida, exceto se , ou seja, a origem! A questão foi isso, te vejo na próxima!
Resposta
Ao longo dos passos.