Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 95
Obtenha, em cada caso, uma equação reduzida da parábola , de vértice e o foco em um dos eixos coordenados, supondo que seja tangente a
Passo 1
Uma equação com vértice na origem terá uma equação da forma de:
Arrumando essa equação da tangente nós teremos:
E a equação da tangente na parábola é igual a:
Comparando as duas nós teremos:
Aplicando na equação da parábola nós teremos:
E como , logo:
Então o valor de será:
Nos dando uma equação igual a:
Passo 2
Já para a equação da tangente para a parábola pelo exercício 92 será:
Arrumando a equação da tangente nós teremos:
Comparando as duas equações nós teremos:
Então:
Jogando esse valor na equação da parábola nós teremos para :
Portanto:
Então o valor de será:
Portanto a equação será:
Passo 3
Na letra simplesmente temos uma equação que passa pelo vértice, então nunca que ela será tangente, ela sempre será uma secante. E na letra temos uma reta e essa reta também não será uma tangente, ou ela será uma reta exterior ou uma secante. As formas podem ser vistas abaixo.
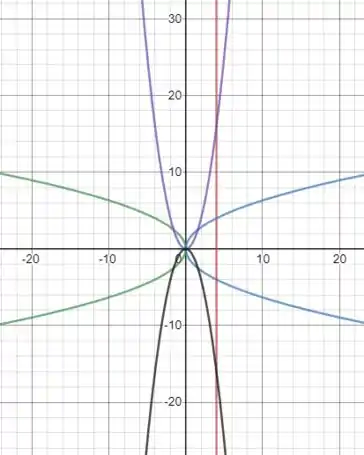
Na forma vemos que a reta até corta o gráfico em apenas um ponto mas ela não será tangente.