Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 26.Exercício - Ex. 13a

Obtenha, em cada caso, uma da superfície gerada pela rotação da curva Γ = Ω 1 ∩ Ω 2 em torno de O x (no item (c), e é o número de Euler).

(a) Ω 1 : y = 0                     Ω 2 : x 2 + z 2 = 1

Passo 1

Devemos obter uma equação da superfície gerada pela rotação da curva em torno de um eixo dado, certo?

A curva que queremos rotacionar é dada pela interseção Ω 1 ∩ Ω 2 . Vamos fazer a representação gráfica dela:

Passo 2

Vamos começar calculando a interseção:

Ω 1 ∩ Ω 2 ⇒ y = 0 ∩ x 2 + z 2 = 1 ⇒ Ω 1 ∩ Ω 2 = 0 ,   0 ,   0 + - cos ⁡ t ,   0 , sin ⁡ t

Passo 3

A interseção acima é uma cônica, deve ser rotacionada em torno de O x . Comecemos escolhendo o ponto C = ( 0 ,   0 ,   0 ) no eixo de rotação. As equações de um paralelo são:

x 2 + y 2 + z 2 = μ 2 x + y + z = λ                  

Passo 4

Momento “bizu aí”.

Um ponto ( a ,   b ,   c ) , pertence à interseção do paralelo com a curva se suas coordenadas satisfazem as relações abaixo:

a 2 + b 2 + c 2 = μ 2 a + b + c = λ                   a = - cos ⁡ t                       b = 0                                                 c = - sin ⁡ t                         ⇒ - cos ⁡ ( t ) 2 + 0 2 + - sin ⁡ t 2 = μ 2 - cos ⁡ t + 0 - sin ⁡ t = λ                                         ⇒ { 1 = μ 2

Passo 5

Por fim, para facilitar a nossa visualização, vamos ilustrar a equação da esfera obtida na resolução acima do sistema:

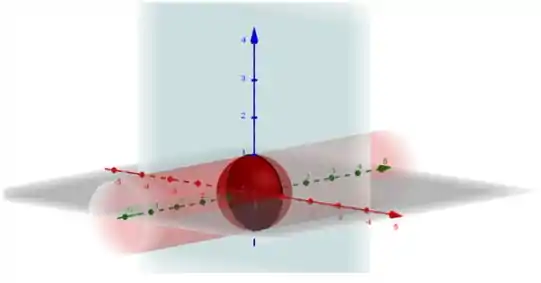
Portanto, encontramos que a equação da superfície gerada pela rotação da curva em torno do eixo O x é a esfera de equação: x 2 + y 2 + z 2 = 1 .

Resposta

x 2 + y 2 + z 2 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. b )z = 9 - x 2 - y 2
Seja O = ( 0,0 , 0 ) . Qual o lugar geométrico dos pontos P = x , y , z tais que O P → 2 = 4 ? Qual figura é representada pela equação x 2 + y 2 = 4 ?
Encontre uma equação em coordenadas cilíndricas da superfície cuja equação em coordenadas cartesianas é dada. d) x 2 + y 2 = z 2
Encontre uma equação em coordenadas cilíndricas da superfície cuja equação em coordenadas cartesianas é dada. c) x 2 - y 2 = 3 z 2
Encontre uma equação em coordenadas cartesianas da superfície cuja equação em coordenadas cilíndricas é dada. c) r 2 c o s ⁡ ( 2 θ ) = z 3