Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 25
Obtenha uma equação que descreva o conjunto , reunião das retas paralelas a que são tangentes a superfície esférica de centro e raio
Passo 1
Imagine um ponto que pertence a esse conjunto junto com a reta paralela dada no enunciado e de forma que esse pertence a esfera. Considere também um ponto de tangência onde:
Então:
E pertence a esfera que pelo enunciado tem equação igual a:
Passo 2
Aplicando então o ponto nós iremos ter:
Abrindo essa equação e agrupando em termos de nós iremos obter:
Fazendo o determinante dessa coisa monstruosa ser nulo (por conta da tangencia) nós iremos ter:
O que pode ser escrito como:
Logo a equação será:
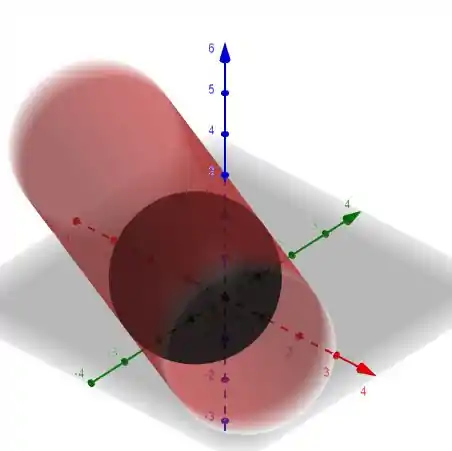
Essa região é uma região cilíndrica e que pode ser vista abaixo (junto com a esfera):
Resposta
Exercícios de Livros Relacionados
Imponha uma condição aos coeficientes a , b , c e d para que o plano π : a x + b y + c z + d = 0 seja tangente à superfície esférica S : x 2 + y 2 + z 2 = ρ 2 .
Determine o centro e o raio da circunferência interseção do plano π : 2 x - 2 y - z + 9 = 0 com a superfície esférica S : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z - 86 = 0 .
Obtenha equações da circunferência Γ de centro G que contém os pontos A e B , nos casos: G = 1,2 , 1 , A = 2,2 , 0 , B = 1,1 , 4 G = 1,1 , 4 , A = 0,3 , 2 , B = 2,3 , 6 G = 2,1 , 1 , A = 1,0 , 2 , B =
Dado os pontos A = 3 , - 2,5 , B = - 1,6 , - 3 e P = 1 , - 4,1 , obtenha equações da circunferência de diâmetro A B que contém P
Prove, no caso (b) da Proposição 24-26, que todo ponto de S 2 , diferente de T , é exterior a S 1 .