Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 12
Obtenha equações planares para as retas
a)
b)
c)
Passo 1
a) Escrevendo equações paramétricas para :
Temos que sumir com o parâmetro para chegarmos em equações planares, certo? Da terceira equação, temos que , vamos substituir nas outras equações:
Então, as equações planares de são:
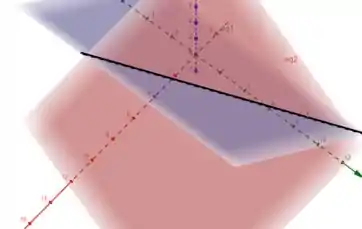
Na figura abaixo, temos os planos e e a intersecção deles, a reta preta, é a reta .
Passo 2
b) Escrevendo equações paramétricas para :
Temos que sumir com o parâmetro para chegarmos em equações planares, certo? Da terceira equação, temos que , vamos substituir nas outras equações:
Então, as equações planares de são:
Passo 3
c) Escrevendo equações paramétricas para :
Temos que sumir com o parâmetro para chegarmos em equações planares, certo? Da segunda equação, temos que , vamos substituir nas outras equações:
Então, as equações planares de são:
Resposta
a)
b)
c)
Atenção, existem várias formas de resolver esse exercício, portanto, dependendo da forma como você resolveu, a sua resposta pode estar diferente das mostradas acima e ainda assim estar correta beleza??
Para conferir a resposta, você pode fazer o seguinte, escolher dois pontos quaisquer das suas retas e substituir nos dois planos, se as equações forem satisfeitas, ta certinho hahaha