Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 17
Sejam e . Determine os pontos de equidistantes de e .
Passo 1
Primeiro vamos escrever um ponto genérico de a partir da sua equação:
Para que o ponto de tenha a mesma distância até e até , vamos usar a fórmula de distância entre pontos:
Como queremos que essas distâncias sejam iguais, vamos igualar as duas belezinha?
Passo 2
Igualando:
Elevando os dois lados ao quadrado pra tirarmos a raíz:
Temos dos dois lados, podemos cortar:
Agora é só abrirmos esses quadrados:
Substituindo no ponto genérico :
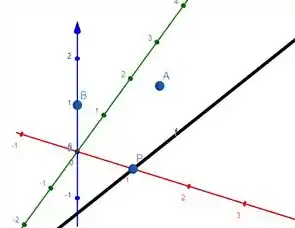
Ah, a reta preta na imagem é a reta :)
Resposta
Exercícios de Livros Relacionados
O ponto P = (x1, y1) pertence à circunferência Γ de centro (a, b) e raio r. Qual é a equação da tangente a Γ no ponto P?
Ache as equações das retas que passam pelo ponto (2, 5) e são tangentes à circunferência de centro O e raio 3.
Escreva, sob a forma ax + by = c, a equação da tangente à circunferência x² + y² = 1 que toca no ponto (x1, y1) dessa curva.
A tangente, no ponto P, à circunferência de centro O e raio 3 é paralela à reta y = −2x + 1. Quais são as coordenadas de P? E se o raio da circunferência fosse 5?
Diz-se que duas circunferências se cortam ortogonalmente quando, em cada ponto da sua interseção, as tangentes respectivas são perpendiculares. Isto ocorre se, e somente se, o quadrado da distância en