Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 2.Exercício - Ex. 9
Obtenha a soma dos vetores indicados em cada caso da Figura 2-9.
a) é um paralelepípedo.
b) e são cubos de arestas congruentes.
c) O cubo tem centro e está dividido em oito cubos congruentes por planos paralelos às faces.
Passo 1
Vamos olhar para a figura do item (a) primeiro. Lembre-se que para somar vetores, você coloca a traseira de um na cabeça do outro. Além disso, podemos mover os vetores livremente mantendo sua direção e sentido. Observe na figura:
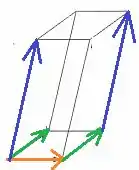
O vetor em laranja foi mantido no lugar. Deslocamos o vetor verde para que sua traseira se encontre com a cabeça do vetor laranja. Fazemos o mesmo com o vetor azul para que sua traseira coincida com a cabeça do vetor verde. Aí, a soma dos três vetores vai ser a ligação da traseira do vetor laranja com a cabeça do vetor azul:
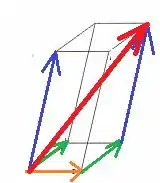
Vemos que a soma dos vetores é igual ao vetor .
Passo 2
Agora vamos para o item (b). Considere o desenho:
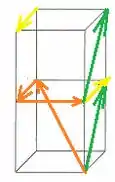
Note que os vetores em amarelo se cancelam. Então esqueça completamente deles! Os vetores que eu desenhei em laranja você não precisa nem deslocar, eles já formam uma fileirinha perfeita. Assim, só precisamos deslocar o vetor verde para a cabeça do último vetor laranja. Daí, é só fazer a ligação direta do começo da cadeia com o final:
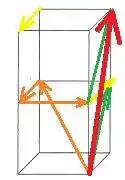
A soma é representada pelo vetor . O vetor também seria uma respostas aceitável. Note que .
Passo 3
Por fim, vamos ao item (c). Observe a figura:
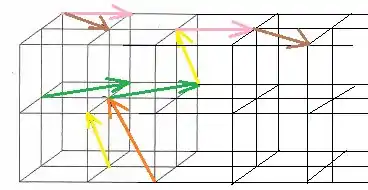
Fomos alinhando na sequência: laranja, verde, amarelo, rosa e marrom. Agora podemos traçar o vetor resultante em vermelho:
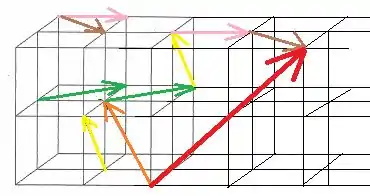
Essa soma é equivalente ao vetor .