Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 21.Exercício - Ex. 8
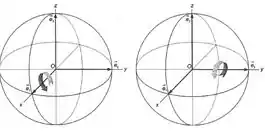
- Deduza as equações da rotação de radianos, em sentido anti-horário, do sistema ortogonal em torno de , e também em torno de (Figura 21-5).
- Interprete as equações , , como equações de rotação de um sistema ortogonal em torno de um dos eixos coordenados.
Passo 1
Quando a questão pede para determinarmos a equação da rotação de radianos, ela está pedindo para escrevermos as coordenadas como função das coordenadas após uma rotação.
Para conseguirmos este sistema, basta realizarmos a seguinte multiplicação de matrizes:
Sendo a matriz de mudança de base. Nosso trabalho será obtê-lo para os casos de uma rotação em torno do eixo e no sentido anti-horário. Para isto, vamos escrever os vetores da nova base ortonormal
Estes vetores estarão no sentido positivo dos eixos após a rotação e nós deveremos escrevê-los como combinação dos vetores da base de .
Passo 2
Vamos começar fazendo uma rotação no eixo . Neste caso, o vetor será igual ao próprio , pois o eixo não mudará de posição.
Fazer um esboço dos novos eixos e dos novos vetores , e após a rotação ajuda bastante na nossa visualização.
Sendo assim, vejamos o que acontece com os vetores após a rotação:
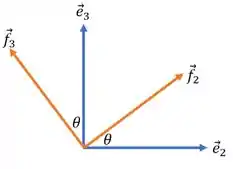
Para escrevermos os vetores como combinação de vetores , basta decompormos os vetores e na direção e sentido de e . Se fizermos isto, iremos obter:
Agora que escrevemos os vetores, já podemos obter a nossa matriz . Como temos três vetores na base, nossa matriz terá 3 colunas. Como temos 3 coordenadas para cada vetor (relativas a , e ), teremos 3 linhas.
Então, para escrever a matriz , basta escrever, de cima para baixo, as coordenadas dos nossos vetores . Na primeira coluna teremos , na segunda e na terceira, . Portanto:
Agora, só fazer a multiplicação de matrizes. Portanto,
Então, escrevendo somente de outra forma, temos as seguintes equações para a rotação de radianos no sentido anti-horário do eixo .
Passo 3
Para a rotação no sentido anti-horário do eixo , iremos fazer o mesmo procedimento feito no passo anterior, a começar pelo esboço dos vetores. Portanto,
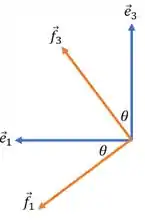
O vetor será igual a , pois o eixo se manteve parado.
1Agora, escreveremos os vetores como combinação de vetores . Decompondo os vetores e na direção e sentido de e . Se fizermos isto, iremos obter:
Agora que escrevemos os vetores, já podemos obter a nossa matriz . Portanto,
Agora, só fazer a multiplicação de matrizes. Portanto,
Então, escrevendo somente de outra forma, temos as seguintes equações para a rotação de radianos no sentido anti-horário do eixo .
Passo 4
Agora, vamos analisar qual rotação as equações nos indicam.
Primeiro, como , sabemos automaticamente que temos uma rotação em torno do eixo . Então, vamos relembrar as equações obtidas no Passo 2.
Vamos comparar as equações de e com as do enunciado da questão. Começando por , temos:
Então, sabemos que e . Isto só ocorre com uma rotação de no sentido anti-horário em torno do eixo .
Resposta
- Rotação em torno do eixo :
- Temos uma rotação de no sentido anti-horário em torno do eixo .
Rotação em torno do eixo :