Obter a equação reduzida resultante de uma translação de eixos, classificar, dar os elementos e representar graficamente as equações:
Passo 1
Para essa questão, temos uma série de elementos que precisamos descobrir:
- Precisamos descobrir qual cônica essa equação representa;
- Determinar os pontos de interesse como Centro, Focos e Vértices;
- Assíntotas caso existam.
Depois de descobertos esses fatores, plotaremos o gráfico.
Passo 2
Para descobrir qual cônica a equação representa. Para isso, vamos completar quadrados.
Passo 3
Completados os quadrados, vamos dividir a equação por para termos o do lado direito da equação.
Portanto, a cônica que estamos trabalhando se trata de uma equação no modelo:
Que é a equação de um hipérbole com eixo paralelo ao eixo com seus parâmetros e dados:
E seu centro
Passo 4
Dada a equação , vamos começar a extrair os pontos de interesse usando os parâmetros que encontramos no Passo 3.
Para acharmos o parâmetro , vamos usar da equação
Passo 5
Para acharmos os vértices e , vamos usar das relações e
. Assim:
Então:
Passo 6
Os Focos são dados pelas relações e . Então:
Logo,
Passo 7
Com os pontos encontrados, vamos achar as assíntotas. Elas são dadas na forma:
Assim:
Passo 8
Com os pontos encontrados e as assíntotas calculadas, vamos plotar o gráfico. Para isso, usamos o Geogebra.
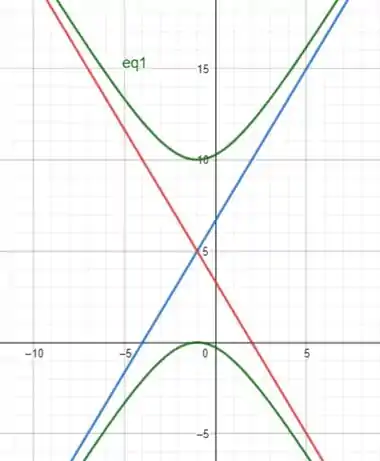
Passo 9
Ainda temos que escrever a equação da cônica da forma com eixos transladados.
Para isso, vamos manter os parâmetros e e escrever na forma:
Passo 10
Para finalizar, vamos escrever os eixos real e imaginário dessa transalação.
O eixo real é dado por . Logo,
O eixo imaginário é dado por . Logo,
Pronto! Era isso que a questão queria!
Resposta
Hipérbole, , eixo real , eixo imaginário , e