Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 30
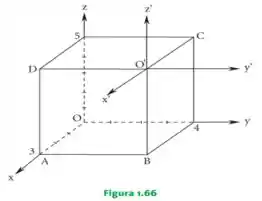
O paralelepípedo retângulo de dimensões está referido ao sistema , conforme a figura 1.66. Considerando um segundo sistema chamado , no qual , e , e sendo um dos vértices do paralelepípedo de acordo com a figura, determinar as coordenadas dos pontos e em relação aos sistemas dados.
Passo 1
Então pessoal, a única coisa que precisamos utilizar aqui para resolver essa questão é a noção de perspectiva, uma vez que temos uma figura . Precisamos descobrir as coordenadas e em relação ao sistema e, em seguida, em relação ao sistema .
Para o sistema temos:
Para o ponto :
Não temos muito o que discutir sobre esse ponto pois é a origem do nosso sistema. Sendo assim:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades, certo? Logo:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Por fim, para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Show! Para o primeiro sistema não foi tão difícil, agora vamos para o segundo!
Passo 2
Para o sistema temos:
Para o ponto :
Diferentemente do que vimos para o primeiro sistema, para esse novo sistema temos que está no octante negativo dos eixos. Sendo assim, temos que:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Para o ponto :
Em temos unidades, em temos unidades e em temos unidades. Logo:
Para o ponto :
Como é nossa nova origem, então:
E essas são nossas coordenadas nos dois sistemas de referência, galera!
Resposta
Para o sistema :
; ; ; ; e
Para o sistema :
; ; ; ; e