Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 72c
O plano intercepta os eixos cartesianos nos pontos A,B e C. Calcular:
C) o volume do tetraedro limitado pelo plano e pelos planos coordenados
Passo 1
Vamos relembrar nossa figura:
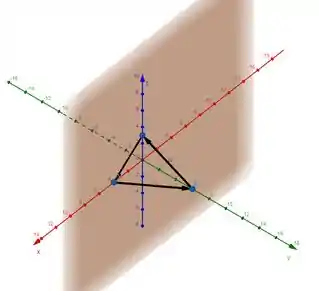
Agora o volume do tetraedro vai ser
Passo 2
lembrando que os pontos que o plano intercepta os eixos são:
A área da base vai ser calculada assim
Onde a base do nosso triangulo vai ser 4 e a altura 3, então temos que:
Passo 3
Agora para calcular o volume vamos fazer
E a altura é o valor de , então ficamos com
Resposta
Exercícios de Livros Relacionados
Achar a distância da origem a cada um dos planosa) π : 3 x - 4 y + 20 = 0
Achar a distância do ponto P ( 2 ,- 3 ,5 ) ao plano π : 3 x + 2 y + 6 z - 2 = 0
Determinar a distância do ponto P = ( 2 ,- 1 ,2 ) a cada um dos planos:a) π : 2 x - 2 y - z + 3 = 0
Determinar a distância do ponto P = ( 2 ,- 1 ,2 ) a cada um dos planos:c) π : 2 x + y = 3
Dado o tetraedro de vértices A = 1 ,2 ,1 ,B = 2 ,- 1 ,1 ,C = ( 0 ,- 1 ,- 1 ) e D = ( 3 ,1 ,0 ) , calcular a medida da altura baixada do vértice D ao plano da face A B C .