1. Fala, galera! Interseção de planos parece ser um negócio bem complicado né? Mas calma que a gente Responde Aí para você. Primeiro, vamos supor que a reta encontre pelo menos um dos três planos coordenados. Para exemplificar: quando a reta corta o plano , então a coordenada . Vamos fazer nas equações dos dois planos e ver se dá para determinar valores válidos de e :

Somando as duas equações, encontramos

Agora, substituímos esse resultado na primeira equação:

Com isso, conseguimos identificar um ponto pertencente a reta .

Agora, precisamos do vetor diretor da reta. E é aí que vem o pulo do gato. Como a reta pertence aos dois planos, então seu vetor diretor será ortogonal a ambos os vetores normais aos planos, que são:

Quando queremos descobrir um vetor ortogonal a outros dois vetores, o melhor caminho é calculando o produto vetorial:



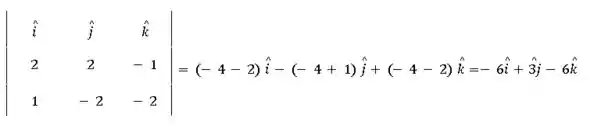
Então, o vetor diretor da reta é proporcional ao vetor que acabamos de descobrir, ou seja, . Lembrando que pertencente a reta , podemos encontrar a equação paramétrica da reta

Passo 2

2. Para saber se a reta tem um ponto de ordenada , vamos substituir esse esse valor na equação da reta, descobrir para qual parâmetro temos essa coordenada e substituir nas demais coordenadas:

Agora, vamos para as outras coordenadas:

Assim, o ponto de ordenada é dado por .