Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 5.Problemas propostos - Ex. 10

Os pontos M 1 ( 2 , - 1,3 ) , M 2 ( 1 , - 3,0 ) e M 3 ( 2,1 , - 5 ) são pontos médios dos lados de um triângulo ABC. Obter equações paramétricas da reta que contém o lado cujo ponto médio é M 1 .

Passo 1

Olá, tudo bem? Vamos resolver junto esse exercício? =D

Para escrever uma equação paramétrica é necessário conhecer um ponto (ou seja, M 1 ) e um vetor diretor da reta. Pra gente ver melhor o que está acontecendo, vou fazer um desenho:

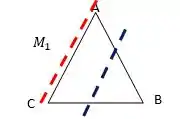
Digamos que o ponto M 1 é o ponto médio entre A e C , e que os outros pontos médios estão sobre outros catetos. Pelo teorema de Tales sabemos que as tretas tracejadas vermelha e azul formam segmentos proporcionais, então podemos dizer que o vetor M 2 M 3 → é paralelo à reta vermelha.

Lembra que precisamos justamente de um vetor que seja paralelo à reta vermelha pra podermos escrever a equação.

Passo 2

Para achar o vetor M 2 M 3 → , podemos ter um que vá do ponto M 2 até o ponto M 3 , então esse vetor é:

M 2 M 3 → = M 3 - M 2 = 2,1 , - 5 - ( 1 , - 3,0 )

M 2 M 3 → = ( 1,4 , - 5 )

Passo 3

O ponto que vou usar vai ser:

M 1 2 , - 1,3

E o vetor:

v → = ( 1,4 , - 5 )

Juntando todas essas informações, podemos escrever as equações paramétricas da reta:

r : x = x 0 + a t y = y 0 + b t z = z 0 + c t

r : x = 2 + t y = - 1 + 4 t z = 3 - 5 t

Espero ter ajudado!

Vamos pra próxima?

Resposta

r : x = 2 + t y = - 1 + 4 t z = 3 - 5 t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Achar as equações da reta que intercepta as retas r 1 e r 2 e é perpendicular a ambas. r 1 :x = 1 + t y = 2 + 3 t z = 4 t , t ∈ R r 2 :x + 1 = y - 1 2 = z + 2 3
Seja r a reta determinada pela interseção dos planos x + y - z = 0e2 x - y + 3 z - 1 = 0 . Ache a equação do plano que passa por A = (1, 0, −1) e contem a reta r.
Achar as equações da reta que intercepta as retas r 1 e r 2 e é perpendicular a ambas.b) x = - 1 + t y = 2 + 3 t z = 4 t,t ∈ R r 2 : x = y - 4 2 = z - 3 3
Sejam r e s retas reversas passando por A = (0, 1, 0) e B = (1, 1, 0) e por C = (−3, 1, −4) e D = (−1, 2, −7), respectivamente. Obtenha uma equação da reta concorrente com r e s e paralela ao vetor V
Seja r 1 a reta que passa pelos pontos A = (1, 0, 0) e B = (0, 2, 0), e r 2 a reta x - 2 = y - 3 2 = z - 4 3 (a) Encontre as equações da reta perpendicular às retas r 1er 2 . (b) Calcule a distância e