Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 3.10 - Ex. 10
Provar que se e são vetores de um espaço vetorial euclidiano, então:
- implica
- implica
Passo 1
- Bora lá, vamos começar desenvolvendo essa expressão. O que a gente tem que saber aqui é que a norma de um vetor ao quadrado é igual ao produto escalar do vetor por ele mesmo. Assim, ó:
- Aqui ele diz que é perpendicular a . Por isso, o produto escalar deles dá . Vamos usar isso aí!
Sabendo disso, vamo que vamo!
Fazendo a distributiva:
Lembra que o produto escalar é comutativo, ou seja, .
Mas se os vetores são ortogonais, , né? Então:
Isso aí é o Teorema de Pitágoras!
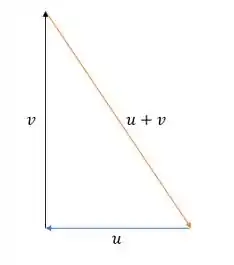
Passo 2
Fazendo a distributiva:
Como os dois são positivos:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam u ev dois vetores não nulos de um espaço vetorial euclidiano. Sendo θ o ângulo de uev , mostrar que u + v 2 = u 2 + v 2 + 2 u v cos θ . (Esta igualdade é conhecida como lei dos cossenos na geom
Mostrar que a soma de dois produtos internos sobre um espaço V também é um produto interno sobre V .
Sejam u = ( x 1 , x 2 ) e v = ( y 1 , y 2 ) vetores genéricos do R 2 e M = a 1 1 a 1 2 a 2 1 a 22 ∈M n ( R ) .Definamos u , v = a 11 x 1 y 1 + a 1 2 x 1 y 2 + a 2 1 x 2 y 1 + a 22 x 2 y 2 .Mostrar que
Sejam e 1 , e 2 , … , e r vetores unitários de um espaço euclidiano tais que e i - e j = 1 (sempre que i ≠ j ) . Calcule o cosseno do ângulo entre dois vetores e i e e j .
Determinar a norma de cada um dos seguintes vetores: u = ( 3,1 , 2,1 ) ∈R 4 ; f t = t 2 + t - 1 , em relação ao produto interno f t , g t = ∫ 0 1 f t g t d t ; A = 1 2 2 1 em relação ao produto do exe