Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 9
- Prove que
Passo 1
Nessa questão, estamos tratando de módulos, que é de forma não muito formal, o comprimento do vetor.
Porém diferentemente das questões anteriores, irei desenhar os vetores ao invés de escrever!
Passo 2
Vamos desenhar o vetor e depois desenharemos o vetor -. Lembrando que ambos são genéricos, então pegarei qualquer vetor.
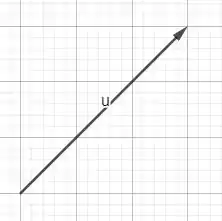
E agora desenharei -.
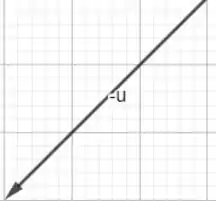
Passo 3
Beleza! Comprimento não tem sentido, é simplesmente o comprimento do segmento orientado! Então tanto , quanto tem a mesma direção, sentidos opostos e mesmo comprimento, opaa!
Ter o mesmo comprimento quer dizer que tem o mesmo módulo hein!
Então, podemos afirmar que:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Mostre que, se A≠ B , então A , B e B , A são de mesmo comprimento, mesma direção e sentido contrário.
Prove que: - - u → = u → u → = - u →↔ u → = 0 →
(a) Faça um desenho ilustrando a proposição anterior no caso em que A , B , CeD são colineares.(b) Prove que ( A , B ) ~ ( C , D ) → ( B , A ) ~ ( D , C ) (c) Prove que A , B ~ C , D → C , A ~ ( D , B
Verifique se é verdadeira ou falsa cada afirmação e justifique sua resposta A B → = C D → ⇒ A , C ~ ( B , D ) A B → = C D → ⇒ A C ∩ B D = ∅ A B → = C D →⇒ A B → = C D A B → = C D → ⇒ A B → = C D → Se
Determinar o valor de n para que o vetor v → = n , 2 5 , 4 5 seja unitário.