Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 3
- (a) Faça um desenho ilustrando a proposição anterior no caso em que são colineares.
(b) Prove que
(c) Prove que
Passo 1
Vamos lá! A proposição que ele pede para desenhar com colinear é:
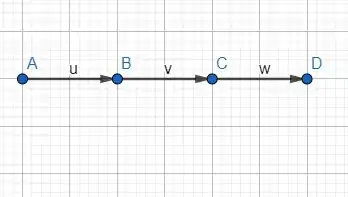
Olha lá! Os segmentos orientados e são equipolares, conforme a proposição pediu! Agora olha os segmentos orientados e . Eles são equipolares, tem a mesma direção, o mesmo sentido e igual comprimento!
Passo 2
Traduzindo isso para a nossa língua ele diz o seguinte:
Se , então
Nesse passo 2, faremos a letra , sempre utilizando segmentos orientados genéricos, pois assim teremos demonstrados os teoremas.
Desenharemos e sabendo que são equipolares, mesmo sentido, mesma direção e mesmo comprimento!
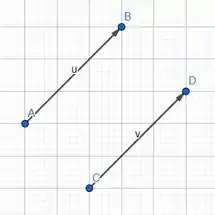
Pronto, traçamos os segmentos equipolentes! Agora vamos traçar os segmentos orientados .
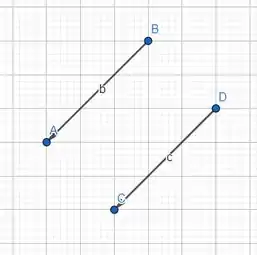
O que esses segmentos orientados tem em comum? Ora!! Tem o mesmo sentido, a mesma direção e mesmo comprimento, então eles são o que? Equipolares!!
Passo 3
Vamos para a próxima demonstração!
Antes vamos traduzir:
Se .
Desenharemos e sabendo que são equipolares, mesmo sentido, mesma direção e mesmo comprimento!
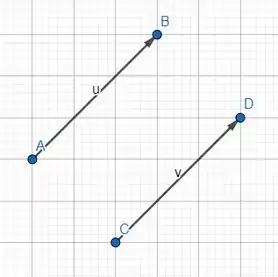
Pronto, traçamos os segmentos equipolentes! Agora vamos traçar os segmentos orientados .
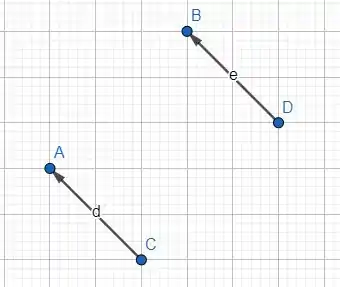
O que esses segmentos orientados tem em comum? Ora!! Tem o mesmo sentido, a mesma direção e mesmo comprimento, então eles são o que? Equipolares!!
Resposta
Ei, a resposta está no passo a passo :)