Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 11
- Verifique se é verdadeira ou falsa cada afirmação e justifique sua resposta
- Se , então existe um único plano contendo
Passo 1
Vou relembrar aqui os conceitos desse capítulo, pois apenas conceitualmente conseguiremos matar todas as alternativas!
Vamos lá.
Segmentos equipolentes são segmentos orientados de mesmo comprimento, mesmo sentido e mesma direção. Indicamos assim:
Um vetor é uma classe de equipolência de segmentos orientados, de grosso modo , pega um conjunto de segmentos orientados e equipolentes! Isso é o vetor
Passo 2
Vamos começar então.
Na letra a) vamos desenhar os vetores e
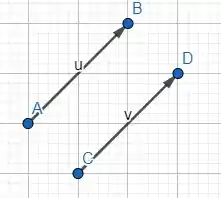
Agora vamos desenhar os segmentos orientados e .
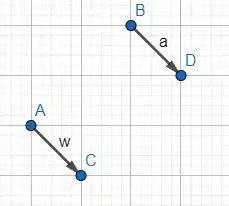
Ora, é verdade! Esses dois segmentos são equipolares.
- Verdadeiro
- Falso
- Falso
- Verdadeiro
- Falso
- Verdadeiro
Vamos para a letra b).
É bem simples imagina que a gente pegue o ponto A igual ao ponto C e o ponto D igual ao ponto B, teremos dois vetores iguais e que a interseção não é vazia!! Se deu ruim para um exemplo é pq é falso!!!
Vamos para a letra c)
Sabemos que dois vetores para serem iguais precisam ter mesmo módulo, mesma direção e mesmo sentido. Então só ter módulo igual não garante que os vetores são iguais, portanto a letra c) é falsa
Passo 3
Continuamos! Letra d)
Se dois vetores são iguais, então eles tem módulos iguais? Sim! É verdade! Para dois vetores serem iguais precisam ter MESMO MÓDULO, mesmo sentido e mesma direção
Letra e)
Se , então existe um único plano contendo
Ora, se tomarmos esses pontos todos sobre uma mesma linha, ou seja colineares, eles não formam um plano e podem ser iguais, então letra e) é falsa!
Para finalizar vamos para a letra f)
Se dois segmentos são equipolares, então eles formam vetores iguais? Simmm! Já que se dois segmentos são equipolares, eles tem mesmo módulo, mesmo sentido e mesma direção!! E isso faz com que dois vetores sejam iguais também!
Resposta
Letra a) Verdadeiro
Letra b) Falso
Letra c) Falso
Letra d) Verdadeiro
Letra e) Falso
Letra f) Verdadeiro