Prove que duas arestas opostas quaisquer de um tetraedro regular são ortogonais.
Passo 1
O exercício quer que mostremos que duas arestas opostas quaisquer de um tetraedro regular são ortogonais. Para isso, vamos visualizar o tetraedro regular:
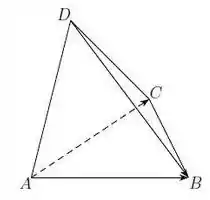
Todas as arestas medem e os ângulos em todas as faces são . Vamos considerar duas arestas opostas: e . Para que essas arestas sejam ortogonais, devemos ter
É isso que vamos tentar demonstrar!
Passo 2
Sabemos que
Assim,
Note que agora cada um dos produtos escalares que sobrou são de arestas numa mesma face, o que é mais fácil de calcular!
Passo 3
O ângulo entre e é , de modo que
Já entre e , o ângulo é :
Portanto,
Assim, vemos que as arestas opostas são ortogonais!
Resposta
Demonstração.