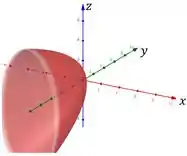
Prove que as equações abaixo descrevem paraboloides elípticos e esboce-os.
Passo 1
Então, vamos verificar que todas as equações são paraboloides. A nossa referença será a equação:
Sabemos que ela é um paraboloide elíptico, se , e com eixo de simetria . Para todas as outras, vamos sempre impor que e vamos fazer mudanças nos sistemas de coordenadas para verificar o que aconteceu com a nossa quádrica.
Nossa primeira equação a ser analisada é:
Cujo eixo de simetria é . A única mudança em relação a nossa referência foi o sinal negativo no segundo membro. Em termos de coordenadas, fizemos a seguinte mudança:
Em termos de esboço do gráfico, o sistema acima significa uma reflexão em torno do plano . Portanto, temos o seguinte esboço:
Passo 2
Agora, vamos fazer a análise em relação aos paraboloides cujo eixo de simetria é o (basta procurar as equações que tem o termo ).
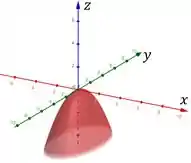
Começando por . Se fizermos interseções com os planos , , temos elipses (o que caracteriza o nome). Em comparação com o nosso sistema de referência, temos a seguinte mudança no sistema de coordenadas:
Tudo confuso, né? A primeira coluna são as coordenadas originais, já a segunda são as novas coordenadas. Conseguimos este sistema fazendo uma rotação de 90 graus no sentido anti horário do eixo e depois uma rotação de 90 graus no sentido horário em torno de . Assim, iremos obter o seguinte esboço:
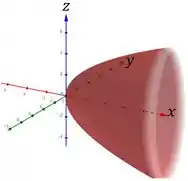
Agora, analisaremos . Continuamos com um paraboloide elíptico, pois as interseções com , nos dão elipses.
A única mudança em relação ao sistema de coordenadas foi fazer ao invés de . O gráfico será uma reflexão do gráfico que fizemos anteriormente em torno do plano . Portanto, temos:
Passo 3
Agora, vamos fazer a análise em relação aos paraboloides cujo eixo de simetria é o (basta procurar as equações que tem o termo ).
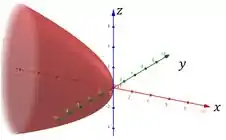
Começando por . Se fizermos interseções com os planos , , temos elipses (o que caracteriza o nome). Em comparação com o nosso sistema de referência, temos a seguinte mudança no sistema de coordenadas:
Tudo confuso, né? A primeira coluna são as coordenadas originais, já a segunda são as novas coordenadas. Conseguimos este sistema fazendo uma rotação de 90 graus no sentido horário do eixo . Assim, iremos obter o seguinte esboço:
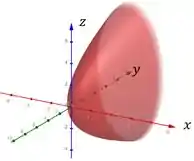
Agora, analisaremos . Continuamos com um paraboloide elíptico, pois as interseções com , nos dão elipses.
A única mudança em relação ao sistema de coordenadas foi fazer ao invés de . O gráfico será uma reflexão do gráfico que fizemos anteriormente em torno do plano . Portanto, temos:
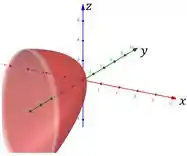
Resposta
A prova do paraboloide elíptico é feita comparando com a equação de referência e fazendo interseções com planos cujo resultado são elipses.
Em relação ao esboço, começando por , temos:
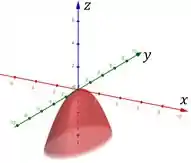
Para , temos:
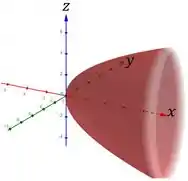
Para , temos:
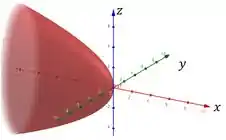
Para , temos:
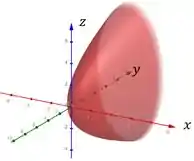
Para , temos: