Prove geometricamente que um quadrilátero é um paralelogramo se, e somente se, suas diagonais se cortam mutuamente ao meio.

Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??

Dizer que as diagonais de um paralelogramo se cortam mutuamente ao meio é dizer que elas se interceptam no ponto médio de ambas. Levando isso em consideração, vamos definir o paralelogramo ABCD mostrado na figura abaixo, com suas diagonais AC e BD se encontrando no ponto E.

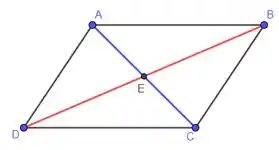
Por definição, um paralelogramo possui lados opostos congruentes, ou seja, AB = CD e AD = BC.

Considerando os lados AB e CD e a diagonal BD temos duas retas paralelas cortadas por uma transversal, conforme podemos ver melhor na figura abaixo:

Notemos que, por definição, os ângulos α e β são alternos internos, e portanto, iguais.

Considerando agora os mesmos lados e a diagonal AC, temos:

Por definição de alternos internos novamente, os ângulos γ e λ são iguais.

Visualizando nosso paralelogramo por completo novamente, temos:

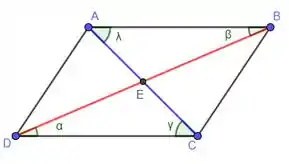
Analisando os triângulos AEB e CED notamos algumas semelhanças, vamos analisá-los lado a lado.

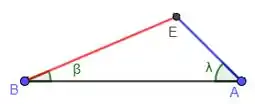
Sabendo que os lados AB e CD são congruentes, que α e β são iguais e γ e λ também, temos aqui um caso ALA de congruência de triângulos.

O que nos permite afirmar que os lados BE e DE são congruentes, portanto, o ponto E é o ponto médio do segmento BD. E ainda também AE e CE são congruentes o que nos leva ao ponto E ser também o ponto médio do segmento AC.

Se o ponto é E ponto médio de AC e BD que são as duas diagonais do nosso paralelogramo, podemos dizer então que as duas diagonais se cortam mutuamente ao meio.