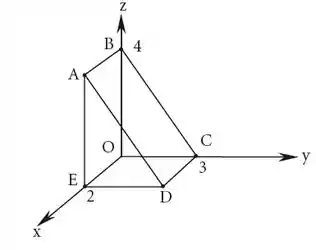
Com base na Figura 5.14, escrever equações paramétricas da reta:
c) e .
Passo 1
Olá, tudo bem? Vamos resolver junto esse exercício? =D
As equações paramétricas de uma reta são:
Onde é um ponto que pertence à reta. E também temos que é o vetor paralelo à essa reta.
Então precisamos encontrar um vetor diretor pra essa reta. E o ponto? Bom, vou usar o ponto .
Pelo desenho os pontos são:
Passo 2
Para achar o vetor , podemos ter um que vá do ponto até o ponto , então esse vetor é:
Passo 3
O ponto que vou usar vai ser:
E o vetor:
Juntando todas essas informações, podemos escrever as equações paramétricas da reta:
Espero ter ajudado!
Vamos pra próxima?