Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 19
Repita o exercício resolvido anterior com os mesmos sistemas de coordenadas, substituindo a equação vetorial por
a)
b)
Passo 1
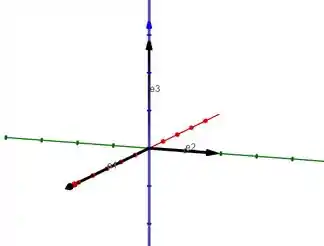
a) A reta , nesse caso passa pela origem e , então ufa, já temos o ponto que a reta passa nos dois sistemas hahahaha
O vetor diretor da reta é , que é paralelo a em e a em .
Logo, a reta vai passar pela origem e vai seguir a direção de em e de em
A reta roxa representa a reta que estamos procurando abaixo: (:
Passo 2
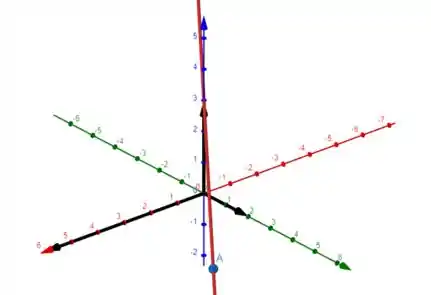
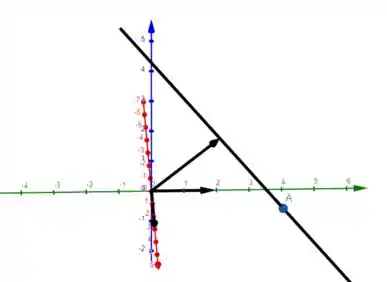
b) O ponto por onde a reta passa equivale a:
em
em
Além disso, o vetor diretor da reta equivale a:
em
em
Então, as retas que procuramos são as retas abaixo:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule a distância do segmento A B à reta s , nos casos(a) A = 1 ,1 ,0B = 2 ,1 ,1s : X = - 1 , - 1 ,6 + λ ( 1 ,4 ,3 )
Calcule a distância do segmento A B à reta s , nos casos(a) A = 2 ,3 ,0B = - 1 ,0 ,6s : X = 0 , - 3 ,- 1 + λ ( 1 ,- 1 ,0 )
Obtenha uma equação vetorial da reta que dista 2 6 de s : X = - 1 ,2 ,3 + λ ( - 1 ,1 ,1 ) , é concorrente r : X = 1 ,1 ,3 + λ 0 ,1 ,1 e está contida em π : x - z + 1 = 0 .
Determine a reta r que contém o ponto A , é paralela ao plano π e dista d da reta s .(b) A = 1 ,3 ,- 1π : x + z = 2s : x - z = y + 2 = z - x + 4 d = 3
Obtenha uma equação vetorial da reta r que contém A = ( 0 ,0 ,3 ) , está contida em π : x + z = 3 e dista 3 de O y .