Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 2
- Prove que .
Passo 1
Não fugiremos da abordagem do livro, com isso não usaremos demonstrações muito pesadas! Apenas utilizaremos o conceito de segmentos orientados para resolver essa questão!
Poderemos desenhar, como o livro pede, nos foi dado os pontos e a ordem deles!
E Vamos traduzir esse enunciado!! Que língua maluca é essa?
O que o enunciado está falando é o seguinte:
Se é equipolente a e é equipolente a , então é equipolente a . Então da primeira afirmação! Tentaremos chegar na segunda!
Passo 2
Ora, vamos desenhar! Primeiro e sendo que esses segmentos orientados são equipolentes! O que é ser equipolente? Mesma direção, mesmo sentido e mesmo comprimento!
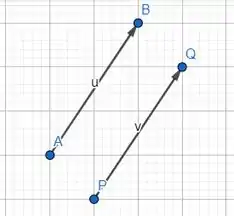
Beleza!!! Já desenhado esses segmentos precisaremos desenhar os outros dois pares de segmentos equipolentes, que são .
Não da mole! Você já desenhou o , não pode mudá-lo agora! Mantenha nos mesmos moldes que fez antes!
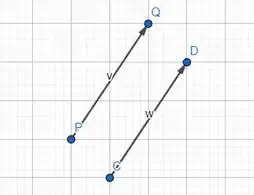
Agora que já desenhamos todos os pares, iremos ver como ficam os três seguimentos juntos, porém no passo 3! Para não ficar muito grande e você conseguir respirar e revisar algo que não tenha entendido.
Passo 3
Nós já desenhamos os três segmentos orientados, mais uma vez! Não os mude agora, você estará alterando tudo que já fizemos.
Botando os três juntos, temos isso aqui ó:
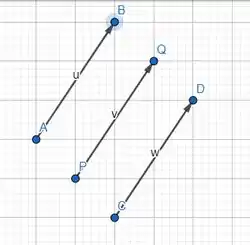
Você percebeu?
Todos esses segmentos são equipolentes! Inclusive o , então chegamos naquilo que queríamos dada a primeira condição chegamos na segunda!
Opa, ainda não percebeu?
Então, vou deixar apenas o .
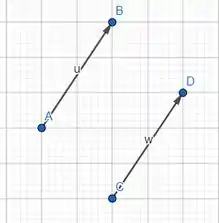
Agora sim! Fica mais fácil de ver que os segmentos são equipolentes!
Resposta
Ei, a resposta está no passo a passo :)