1. Verifique se é verdadeira ou falsa cada afirmação e justifique sua resposta

3. ////
4. .

Continuando, vamos para a letra b).

Primeiro tentaremos provar a ida, que é se os segmentos orientados são equipolares, então os vetores são iguais.

A ideia é você sempre lembrar da definição de vetores, que são o conjunto de segmentos orientados equipolares. Então se dois segmentos são equipolares, eles representam um mesmo vetor, e já que representam o mesmo vetor, podemos afirmar que tem o mesmo sentido, mesma direção e mesmo módulo!!

Portantoooo! Com todas essas características iguais, podemos afirmar que esses vetores são iguais!

Agora precisamos provar o inverso, pois essa é uma relação de vai e vem .

A volta é a seguinte se os vetores são iguais, então são equipolares.

Vamos lá, vamos usar agora a ideia de igualdade entre dois vetores, se dois vetores são iguais, eles tem mesmo sentido, mesma direção e mesmo módulo.

O vetor é um conjunto de segmentos orientados equipolares, então, podemos afirmar que os segmentos são equipolares.

Vamos para a letra c), agora:

Ele diz que se dois segmentos são paralelos, então os vetores que tem a mesma origem e mesma extremidade que eles são paralelos.

Ora, um segmento fica determinado por dois pontos, inclusive o segmento orientado, então se esses segmentos são paralelos, os segmentos orientados correspondentes também serão paralelos.

Ainda não chegamos nos vetores, mas toda vez que provamos para segmentos orientados, estamos falando de vetores também. Então, podemos afirmar que se os segmentos orientados são paralelos, seus vetores também serão.

Logo, a letra c) é verdadeira.

Para finalizar, vamos para a letra d)

Ele fala que se os vetores são iguais, então as origens são iguais e as extremidades também serão.

Vou desenhar dois vetores iguais e que não tenham origens iguais nem mesmo extremidades iguais .

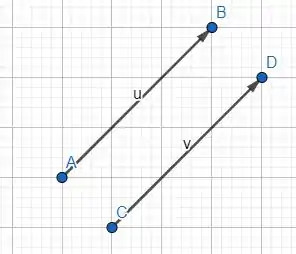
Pronto!! Esses dois vetores são iguais, mas não tem mesma origem nem mesmo extremidades iguais. Então, podemos afirmar que é falsa a letra d).