Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 38
Prove que:
a)
b)
c) as diagonais de um paralelogramo têm comprimentos iguais se, e somente se, o paralelograma é um retângulo.
Passo 1
Para resolver esse problema, vamos usar as seguintes relações:
Essas relações foram mostradas no exercício resolvido 9-11.
Assim, o item (a) é imediato:
Portanto,
Provamos assim o item (a)!
Passo 2
Para o item (b) nós usamos o resultado do item (a). Como a norma de qualquer vetor é não negativa, vale
Mas usando o resultado do item (a):
Assim está provado o item (b)!
Passo 3
Para o item (c), consideremos o paralelogramo da figura a seguir:
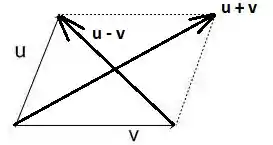
As diagonais terem o mesmo comprimento é equivalente a
Mas provamos no item (b) que isso é equivalente a
Portanto, os lados do paralelograma são perpendiculares: trata-se de um retângulo!
Note que cada item do problema serve para guiar a demonstração final do item (c)!
Resposta
Demonstração.