Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 55
- Prove que uma reta paralela ao eixo de uma parábola tem com ela um único ponto comum
- Prove que, se pertence a região focal da parábola , então qualquer reta que contém e não é paralela ao eixo da parábola é secante a .
Passo 1
Em uma parábola nós temos que o eixo dessa parábola é o próprio eixo então para uma reta paralela ao eixo nós teremos a seguinte figura.
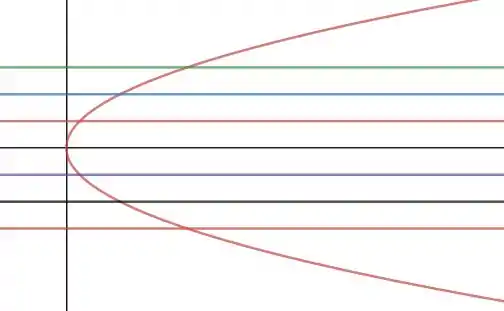
Todas essas retas paralelas cortam a parábola em apenas um ponto, tal como uma equação genérica igual a:
Onde eu digo um ponto qualquer e um tamanho qualquer e depois digo que esse vetor é paralelo ao eixo , ou seja ele tem direção . Isso me dará a equação genérica de todas as retas paralelas ao eixo , que é o eixo dessa parábola.
Passo 2
- Sejam e , em relação a um conveniente sistema ortogonal de coordenadas. Como pertence a região focal, ; utilize para provar que , qualquer que seja o vetor tal que
Como dissemos no passo anterior a equação dessa parábola é algo como e é um ponto com coordenadas iguais a e a equação do determinante dessa parábola é dado por:
E por estar na região focal então , onde o de qualquer ponto da parábola em , ou seja
Tal como foi provado na questão 51, então o termo é negativo o que anula com o sinal e nos dá , logo se não for zero (que daria os vetores paralelos ao eixo , e não nos daria uma equação do segundo grau para ) nós teremos com certeza uma secante.