Um babuíno de altura circula por uma montanha, cujo perfil é a parte da hipérbole de equação contida no primeiro quadrante. Um caçador, de espingarda, arma tocaia no ponto . Determine o trecho do perfil em que o babuíno estará seguro.
Passo 1
Vamos desenhar o que está sendo dito no enunciado para que não aconteça nenhuma confusão:
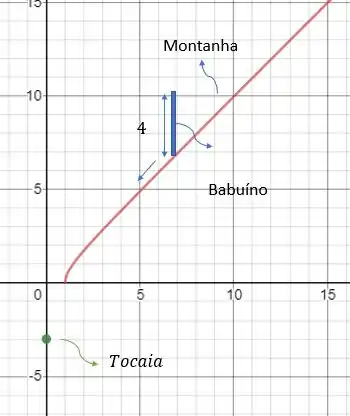
Aí basicamente ele quer saber em que ponto dessa montanha a cabeça do babuíno deverá estar para que o caçador consiga uma reta uma tangente com essa montanha para atingir o babuíno.
A equação da reta tangente será de:
Onde é o ponto de tangência, e como esse ponto está na elipse, logo:
E aplicando o ponto na primeira equação nós iremos ter:
Logo:
Porém somente estaremos interessados no ponto positivo em . Ou seja o ponto de tangencia está em:
Portanto a equação da reta tangente será:
Passo 2
Agora o ponto da elipse que está a uma distância de (na vertical) da reta tangente da elipse será (igualando o x da hipérbole com o x da reta:
Onde , logo:
Isso nos dá uma equação do segundo grau igual a:
Porém só nos interesse a parte positiva, então o que o babuíno deve estar será em:
Não sei se ficou claro, mas já temos nossa região, para isso vamos desenhar tudo que dissemos até aqui. O traçado do tiro, a posição do macaco na montanha e o ponto do tiro.

O traçado é a linha roxa e o ponto de baixo é a posição limite do babuíno na montanha e o ponto de cima é o tiro na cabeça do animal. Então se o babuíno continuar a circundar a montanha ele estará totalmente seguro em um se ele estiver em ele já começa a ter perigo.
A dificuldade dessa questão é ver qual a região que o animal está, se ele estivesse abaixo da curva qualquer ângulo seria fácil pro atirador, e a questão tem que ter dificuldade hhaahah a outra é sobre a informação da altura do animal, essa eu confesso que tive dificuldade de entender mas entenda algo como se o macaco estivesse andando na normal a montanha e não no chão, como se todo o corpo dele estivesse andando pela montanha.