Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 6
Prove que o segmento que une os pontos médios dos lados não-paralelos de um trapézio é paralelo às bases, e sua medida é a média aritmética das medidas das bases.
Passo 1
Vamos usar como ilustração a figura abaixo. Ela ilustra o trapézio ABCD, sendo M e N os pontos médios, respectivamente, de AD e BC.
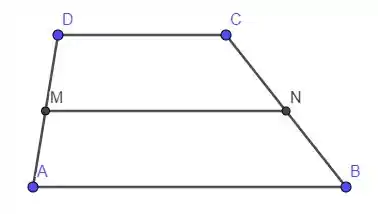
Antes de atacarmos o problema vamos recapitular o que queremos mostrar:
1 - Mostrar que o segmento que liga os pontos médios é paralelo às bases, ou seja,
e .
2 - Mostrar a medida do segmento é a média aritmética das medidas das bases, ou seja,
Show de bola? Então vamos começar!
Para mostrar que o segmento que liga os pontos médios é paralelo às bases, se você reparar, no enunciado ele de cara nos dá uma informação que será bem importante para iniciarmos a questão: a palavrinha ponto médio.
Passo 2
Sabemos pelo enunciado que M e N são pontos médios. Ou seja,
Sabendo disso, vamos calcular a distância entre os pontos M e N:
Como podemos dizer que existe um escalar (diferente de zero, pois e não são vetores nulos) de forma que,
Sendo assim, podemos substituir o valor de lá na distância entre os pontos M e N. Vai ficar assim:
Dando aquela arrumada marota, ficamos com:
Como , onde , temos que .
Já que também temos que , teremos então que .
Passo 3
Para mostrar que a medida do segmento é a média aritmética das medidas das bases vamos aproveitar essa informação que achamos anteriormente,
Note que
Essa divisão não tem problema, pois os vetores não são nulos. Além disso, como esses vetores possuem o mesmo sentido, temos que k é positivo. Desse modo, podemos apenas escrever que:
Portanto, teremos que
Note que o numerador e o denominador da fração são escalares positivos. Portanto, podemos retirar o módulo e ficar apenas com
Logo,
Resposta
Ei, a resposta está no passo a passo :)