Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 11b
O quadrilátero ABCD (Figura 2.16) é um losango de lado 2. Calcular:
b)
Passo 1
Vamos primeiro lembrar como a gente calcula esse produto!
Agora vamos destacar quem são esses vetores e
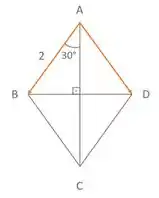
Passo 2
Agora que a gente tem mais claro quem são esses vetores, podemos perceber que o ângulo que eles fazem é de 60°, então temos que:
Como o lado do losango é 2, temos que o módulo dos dois vetores também é 2
Resposta
Exercícios de Livros Relacionados
Dados os vetores a →=( 1 , - 2 , - 1 ) e b →=( 0 , - 3,1 ) , determine um vetor u → , sabendo que u → é ortogonal a a → e b → , | u | →=315 e o ângulo formado por u → e o vetor ( 1,0 , 0 ) é agudo.
u →=( 2,1 , - 3 ) e v →=( 1,2 , 1 ) . Se w →=u→+λ v → , determine λ para que u→ e w → sejam ortogonais.Determine o coseno do ângulo que u→ forma com v → .
Sejam O A →=( 1,1 , 3 ) , O B →=( 3,2 , 2 ) e O C →=( 1,0 , - 4 ) .Ache as coordenadas de todos os vetores determinados pelos pontos O, A, B e C.Demonstre que os 4 pontos (não necessariamente na ordem
Ache um vetor v → que forma ângulos iguais com ( 1,0 , 0 ) e ( 0,0 , 1 ) é ortogonal a u →=( 2 , - 2,2 ) , | v | →= 24 , sendo agudo o ângulo que v → forma com ( 0,1 , 0 ) .
Ache um vetor de norma 1, ortogonal a u →=( 1 , - 3,1 ) e a v →=( - 3,3 , 3 ) .