Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 27a
Repita o exercício resolvido anterior com os mesmos sistemas de coordenadas, substituindo a equação vetorial por:
(a)
Passo 1
Antes de iniciarem essa questão, é importante que vocês deem uma olhada no Exercício Resolvido 14-16, beleza?
Para esboçar os planos, eu utilizei o SolidWorks, mas fazer no papel também é válido, o mais importante é ter a noção de como fazer.
Então, vamos lá!
Passo 2
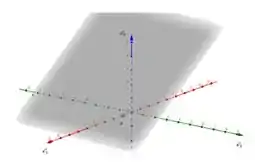
Para esboçar geometricamente duas retas com base em uma equação vetorial dada, consideram-se seus vetores diretores.
Portanto, o plano contém o ponto e possui vetores diretores de e ao vetor :
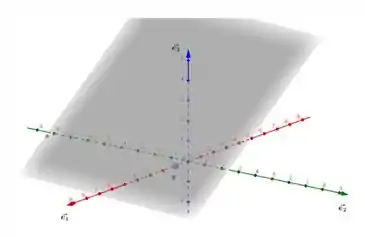
Passo 3
Portanto, o plano contém o ponto e possui vetores diretores de e ao vetor :
Resposta
(a)
Exercícios de Livros Relacionados
a) Prove que o lugar geométrico dos pontos que são equidistantes de A = ( 2 ,1 ,1 ) , B = ( - 1 ,0 ,1 ) e C = ( 0 ,2 ,1 ) é uma reta e obtenha uma equação vetorial para ela.b) Mostre que a reta do ite
Obtenha uma equação geral do plano π que contém o ponto P e é perpendicular à reta r .a) P = ( 0 ,1 ,- 1 ) r : X = 0 ,0 ,0 + λ( 1 ,- 1 ,1 ) b) P = ( 0 ,0 ,0 ) r contém A = ( 1 ,- 1 ,1 ) e B = ( - 1 ,1
São dados o ponto P( 2 ,1 ,0 ) , a reta r : X = 0 ,0 ,0 + λ 2 ,1 ,0 e o plano π : x + y + z - 3 = 0 . Para cada ponto Q, seja Q’ a projeção ortogonal de Q sobreπ . Determine os pontos Q da reta r tais
Determine as coordenadas da projeção ortogonal do ponto P sobre o plano π , nos casos:a) P = ( 1 ,0 ,1 ) π : x - 2 y + 4 z = 1 b) P = ( 4 ,0 ,1 ) π : 3 x - 4 y + 2 = 0
Para que valores de m a reta r : x - 1 m = y 2 = z m é transversal ao plano π : x + m y + z = 0 ?