Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 17.Exercício - Ex. 24
São dados o ponto , a reta e o plano Para cada ponto Q, seja Q’ a projeção ortogonal de Q sobre. Determine os pontos Q da reta r tais que o triângulo PQQ’ tenha área
Passo 1
Animados galerinha ??
Quando
Então o ponto P faz parte da reta r, certo?
Quando olhamos no plano:
Se analisarmos o ponto P aqui:
Então o ponto pertence a reta e ao plano, ok?
Vamos desenhar o que está acontecendo:
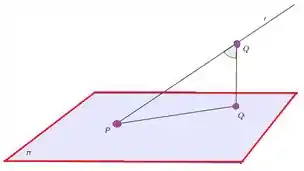
Como nós achamos o vetor podemos achar também o comprimento de um dos lados, querem ver como??
Simples!!
Basta usarmos:
Como o ponto Q pertence à reta r, queremos determinar o vetor Se Q pertence a reta:
Se já temos P e Q podemos achar o vetor:
Agora podemos achar o módulo do vetor
Olhando nosso plano:
Conseguimos achar
E seu módulo:
Agora é só achar o ângulo:
Sendo assim:
Passo 2
Conseguimos achar um comprimento de lado do triângulo, mas a área é dada como:
Então nós só precisamos do valor de seno, que facilmente podemos descobrir usando a relação:
Substituindo:
Quando
E quando
E fiiiim !!