Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 5.Problemas propostos - Ex. 18h
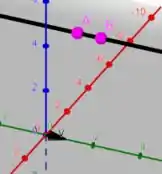
18. Representar graficamente as retas de equações:
h)
Passo 1
Assim como estudamos no capítulo em questão do Winterle, para podermos representar graficamente as retas de equações que nos foram dadas, temos que encontrar o vetor diretor da reta e dois pontos em que a reta passa!
Para determinarmos o vetor diretor temos que encontrar dois pontos da reta ( e ) primeiro, pois o vetor pode ser encontrado assim:
Então let’s go!
Passo 2
Para determinarmos dois pontos, basta utilizarmos os conceitos que aprendemos em funções. Vamos substituir dois valores de , se liga:
Para , temos:
Então um ponto é . Agora para , temos:
Então outro ponto é . Sendo assim, o vetor diretor seria:
E a representação da reta ficaria dessa forma:
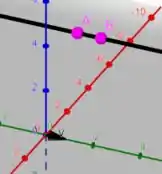
No qual o eixo em vermelho é , o eixo em verde é e o eixo em azul é .
Resposta
Representação da reta:
