Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 8.Problemas Propostos - Ex. 3a
Representar graficamente as seguintes superfícies cilíndricas:
Passo 1
Perceba que o que acontece aqui, teremos (já que não aparece na fórmula). Analisando a nossa fórmula, teremos que indica que temos uma parábola, e o sinal negativo nos mostra que temos uma parábola com a concavidade negativa.
Temos então uma parábola em .
Se :
Isso significa que a parábola toca o eixo em :
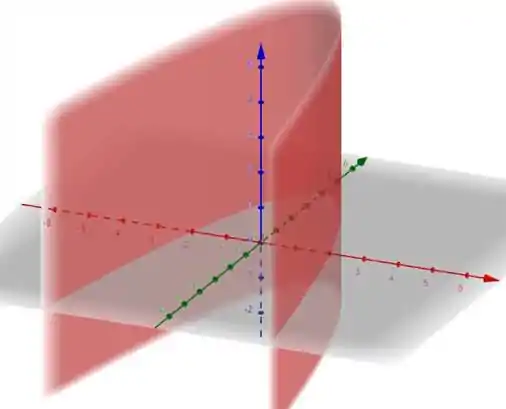
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. e )z 2 = x 2 + y 2
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados. n )z = 9 - y 2 ,- 4 ≤ x ≤ 4
8. Identificar a superfície S e a sua interseção com o plano π dado. Representar graficamente esta interseção no plano π . b )S : 4 x 2 + 4 y 2 - z 2 = 0eπ : z = 4
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados. m )y 2 - x 2 = 16 ,0 ≤ z ≤ 4
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados. l )y 2 + 4 z 2 - 4 = 0 ,- 4 ≤ x ≤ 6