Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7e
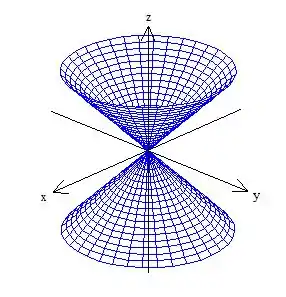
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.
Passo 1
Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:
POXA! Eu não sei se você está com as mesmas impressões que eu, mas se estiver, vai estar desconfiado de que esta equação nos representa um cone. Vamos ver se é isso mesmo?
Passo 2
Sabemos pela teoria, que a equação do cone (ao redor do eixo ) pode ser dada pela equação geral:
A nossa equação é parecida:
Só que com , logo, de fato é um cone que temos aí e ao redor do eixo !
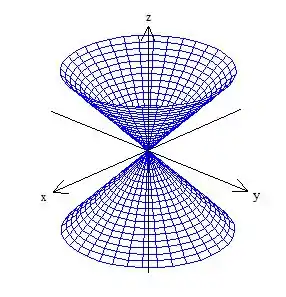
Resposta
Cone ao redor do eixo :
Exercícios de Livros Relacionados
Dadas as equações da curva diretriz determine a equação da superfície cônica que tem vértice na origem O = (0, 0, 0).a) x 2 + y 2 = 4ez = 2
Mostre que cada uma das equações representa uma superfície cilíndrica e determine a equação da curva diretriz e um vetor paralelo as retas geratrizes. b) x 2 + y + 5 z 2 + 2 x z + 4 y z - 4 = 0
Determine a equação da superfície de revolução gerada pela rotação da curva dada em torno do eixo especificado. c) y z = 1ex = 0 em torno do eixo z .
Determine a equação da superfície de revolução gerada pela rotação da curva dada em torno do eixo especificado. d) z = e xey = 0 em torno do eixo z .
Mostre que cada uma das equações representa uma superfície de revolução e determine o seu eixo de revolução e a equação de uma curva geratriz. b) x 2 + z 2 = 4