Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 11

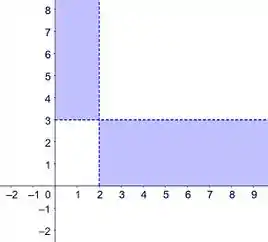
Represente graficamente o conjunto Ω dos pontos X de coordenadas positivas para os quais existe uma elipse contendo X e P = 2,3 , de centro O e focos em um dos eixos coordenados.

Passo 1

O objetivo desta questão é fazer um gráfico do conjunto dos pontos X = h , k . Vamos encontrar uma série de restrições para estes pontos para poder esboça-los graficamente.

Primeiro, sabemos que estes pontos possuem apenas coordenadas positivas. Logo, a nossa primeira restrição é h > 0 e k > 0 . Já sabemos então que estamos trabalhando somente no primeiro quadrante.

Continuando, estamos trabalhando com uma elipse com centro em O e focos em um dos eixos coordenados. Portanto, os pontos satisfazem a seguinte equação da elipse:

x 2 p + y 2 q = 1

E como é uma elipse, obrigatoriamente, sabemos que p > 0 , q > 0 e p ≠ q . Estas três restrições serão importantes para o futuro próximo! Vamos trabalhar com elas para conseguir outras restrições de h e k para conseguir esboçar o conjunto Ω .

Passo 2

Agora, temos que trabalhar com as equações. Sabemos que o ponto X e P = 2,3 pertencem a elipse. Portanto, satisfazem a sua equação. Então, temos o seguinte sistema:

h 2 p + k 2 q = 1 4 p + 9 q = 1 ⟹ q h 2 + p k 2 p q = 1 4 q + 9 p p q = 1 ⟹ q h 2 + p k 2 p q = 1 p = 4 q q - 9

Da segunda equação, conseguimos isolar a variável p em função de q . Fizemos isto com o objetivo de escrever h e k como função de p e q , pois conhecemos mais informações (restrições) sobre eles.

Agora, vamos substituir essa relação na nossa primeira equação. Portanto,

q h 2 + k 2 ⋅ 4 q q - 9 4 q 2 q - 9 = 1

q h 2 ⋅ q - 9 + 4 q k 2 q - 9 4 q 2 q - 9 = 1

q h 2 ⋅ q - 9 + 4 q k 2 4 q 2 = 1

h 2 ⋅ q - 9 + 4 k 2 4 q = 1

h 2 ⋅ q - 9 + 4 k 2 = 4 q

4 q - h 2 q = 4 k 2 - 9 h 2

q = 4 k 2 - 9 h 2 4 - h 2

Substituindo o valor de q naquela relação entre p e q . Então, temos:

p = 4 q q - 9 = 4 ⋅ 4 k 2 - 9 h 2 4 - h 2 4 k 2 - 9 h 2 4 - h 2 - 9 = 4 ⋅ 4 k 2 - 9 h 2 4 - h 2 4 k 2 - 9 h 2 - 9 4 - h 2 4 - h 2

p = 4 ⋅ 4 k 2 - 9 h 2 4 k 2 - 9 h 2 - 36 + 9 h 2 = 4 ⋅ 4 k 2 - 9 h 2 4 k 2 - 36

p = 4 ⋅ 4 k 2 - 9 h 2 4 ⋅ k 2 - 9 = 4 k 2 - 9 h 2 k 2 - 9

Passo 3

Conseguimos relacionar p e q com as variáveis h e k . O sistema que obtivemos foi:

q = 4 k 2 - 9 h 2 4 - h 2 p = 4 k 2 - 9 h 2 k 2 - 9

É agora que iremos aplicar as nossas relações. Primeiro, sabemos que p > 0 e q > 0 .

Temos duas possibilidades: o numerador 4 k 2 - 9 h 2 > 0 ou menor do que 0. Então, vamos analisar separadamente.

Se 4 k 2 - 9 h 2 > 0 , o denominador também deve ser positivo. Portanto,

4 - h 2 > 0 k 2 - 9 > 0 ⟹ 2 - h 2 + h > 0 k - 3 k + 3 > 0

Como h > 0 e k > 0 , para que o denominador seja um numero positivo, devemos garantir que:

2 - h > 0 k - 3 > 0

Ou, multiplicando ambas as equações, para conseguirmos uma única relação,

2 - h k - 3 > 0

Agora vamos analisar o segundo caso: se 4 k 2 - 9 h 2 < 0 . Para este caso, o denominador também deve ser negativo, para que a razão seja um número positivo. Portanto,

4 - h 2 < 0 k 2 - 9 < 0 ⟹ 2 - h 2 + h < 0 k - 3 k + 3 < 0

Como h > 0 e k > 0 , para que o denominador seja um numero positivo, devemos garantir que:

2 - h < 0 k - 3 < 0

Ou, multiplicando ambas as equações, para conseguirmos uma única relação,

2 - h k - 3 > 0

Que é a mesma relação que obtivemos para o caso anterior!

Já sabemos que h > 0 , k > 0 e 2 - h k - 3 > 0 . Só nos falta utilizarmos uma única relação: p ≠ q .

Portanto,

p ≠ q

4 k 2 - 9 h 2 4 - h 2 ≠ 4 k 2 - 9 h 2 k 2 - 9

1 4 - h 2 ≠ 1 k 2 - 9

k 2 - 9 ≠ 4 - h 2

k 2 + h 2 ≠ 13

Portanto, as restrições para h e k são:

h > 0 k > 0 2 - h k - 3 > 0 k 2 + h 2 ≠ 13

Passo 4

Por fim, só nos resta esboçarmos o conjunto Ω . Portanto, temos o seguinte conjunto:

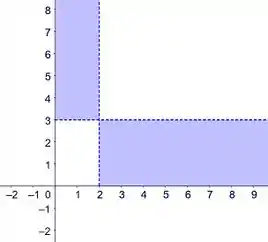
E assim resolvemos a questão.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as funções dadas f e g defina f - g e determine o domínio da função resultante. f x = x 2 - 9 e g x = x + 5
Para as funções dadas f e g defina g ο f e determine o domínio da função resultante. f x = x e g x = 1 x 2
Para as funções dadas f e g defina g ο f e determine o domínio da função resultante. f x = 1 x - 3 e g x = x x + 1
Para as funções dadas f e g defina f ο g e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4
Ache a equação da reta tangente à elipse 4 x 2 + 9 y 2 = 72 no ponto ( 3 ,2 ) .