Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 20.Exercício - Ex. 4a

Obtenha os pontos da reta r que equidistam de A e B e comente as peculiaridades geométricas de cada caso.

a) r : x - 1 = 2 y = z                       A = 1 ,   1 ,   0                       B = ( 0 ,   1 ,   1 )

Passo 1

a) Vamos começar escrevendo a reta r de uma forma visualmente mais bonitinha, pra aí conseguirmos arrancar um ponto genérico dela hehe da sua equação temos:

x - 1 = 2 y

x = 2 y + 1

Além disso, temos que

z = 2 y

Logo, nossa reta tem o formato:

x ,   y ,   z = ( 2 y + 1 ,   y ,   2 y )

x ,   y ,   z = 1 ,   0 ,   0 + t . ( 2 ,   1 ,   2 )

Portanto, um ponto genérico da reta r é

P = ( 1 + 2 t ,   t ,   2 t )

Passo 2

Queremos os pontos P = ( 1 + 2 t ,   t ,   2 t ) de r que tenham a mesma distância até A = ( 1 ,   1 ,   0 ) e até B = ( 0 ,   1 ,   1 ) , então:

d P , A = d ( P ,   B )

Usando a fórmula de distância entre pontos:

1 + 2 t - 1 2 + t - 1 2 + 2 t - 0 2 = 1 + 2 t - 0 2 + t - 1 2 + 2 t - 1 2

2 t 2 + t - 1 2 + 2 t 2 = 1 + 2 t 2 + t - 1 2 + 2 t - 1 2

Desenvolvendo os produtos notáveis:

4 t 2 + t 2 - 2 t + 1 + 4 t ² = 1 + 4 t + 4 t 2 + t 2 - 2 t + 1 + 4 t 2 - 4 t + 1

9 t 2 - 2 t + 1 = 9 t 2 - 2 t + 3

Elevando os dois lados ao quadrado:

9 t 2 - 2 t + 1 = 9 t 2 - 2 t + 3

Eliminando os termos em comum dos dois lados, temos:

1 = 3

Opa, o nosso t sumiu e chegamos em uma desigualdade!!

O que isso quer dizer?? Que não existem pontos de r equidistantes a A e B . Isso acontece porque r é paralela ao plano mediador de A e B :

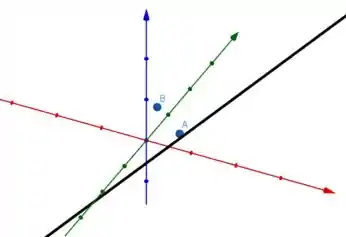
Resposta

a) Não existe ponto de r equidistante a A e B

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha equações do lugar geométrico dos pontos de E ³ ³ que equidistam de A , B e C e determine as coordenadas do circuncentro do triângulo A B C , nos casos:a) A = 0 ,2 ,1 B = 2 ,2 ,- 1 C = ( - 2 ,0
Obtenha equações do lugar geométrico dos pontos de E ³ ³ que equidistam de A , B e C e determine as coordenadas do circuncentro do triângulo A B C , nos casos:b) A = 3 ,0 ,1 B = 2 ,1 ,0 C = ( 4 ,- 1 ,
Prove que o lugar geométrico dos pontos de E ³ ³ que equidistam de três pontos dados, A ,B e C é:a) uma reta perpendicular ao plano A B C , se os três pontos não são colineares;b) o conjunto vazio, se
Sejam p um número real positivo, A e B dois pontos tais que d A , B = p , e n , um número real qualquer. Prove que o lugar geométrico dos pontos X de E 3 tais que d X , A 2 - d X , B 2 = n é um plano
Mostrar que o ponto P 1 ( 2,2 , 3 ) é equidistante dos pontos P 2 ( 1,4 , - 2 ) e P 3 ( 3,7 , 5 ) .