Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 1.Problemas Propostos - Ex. 3b
Sabendo que o ângulo entre os vetores e é de , determinar o ângulo formado pelos vetores:
e
Passo 1
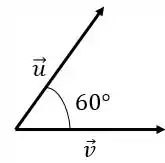
Vamos primeiro desenhar os vetores e respeitando o ângulo entre eles.
Passo 2
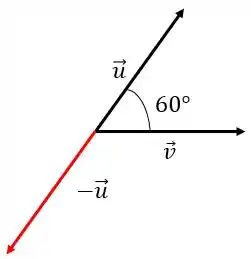
Vamos inverter o vetor para obtermos
Passo 3
O ângulo formado por e é suplementar ao ângulo formado por e . Portanto,
Resposta
Exercícios de Livros Relacionados
(b) No quadrilátero ABCD (eventualmente reverso, como na Figura 5-2 (b)), M divide (A,B), N divide (C,B), P divide (C,D) e Q divide (A,D), todos na razão r. Prove que o quadrilátero MNPQ é um paralelo
Dado o triângulo ABC, sejam P, O e R pontos tais que A B → = α P B → ,A C → = β Q C → ,α P R → = β Q R → . Prove que, se α ≠ 1 , então B, C e R são colineares.
(a) Mostre que o baricentro de um triângulo ABC (ponto comum às três medianas do triângulo) é também o baricentro dos pontos A, B, C, como foi definido no Exercício 4-13 .
Sejam A, B, C e D vértices de um quadrado, E um ponto de AD e F um ponto de CD, tais que o triângulo CEF seja equilátero. Calcule a razão em que E divide (A,D) e a razão em que F divide (D,C).
Sejam s 1 e t 1 duas retas concorrentes em B, tangentes à circunferência de centro A e raio r 1 , (Figura 5-10). Com centro em um ponto P da semi-reta de origem B que contém A, traça-se a circunferênc