Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 9a

(a) Mostre que o baricentro de um triângulo ABC (ponto comum às três medianas do triângulo) é também o baricentro dos pontos A, B, C, como foi definido no Exercício 4-13 .

Passo 1

Bora lá!

Devemos mostrar que o baricentro (centroide) do triângulo ABC também é baricentro de seus pontos.

O conceito de baricentro para n pontos distintos já foi definido no Exercício 4-13, ok? Mas vamos relembrar.

O baricentro será representado pelo ponto G tal que:

∑ i = 1 n G A → i = 0 →

Ou seja, precisamos provar que a soma dos vetores A G → + B G → + C G → = 0 , certo?

Então, mão na massa!

Passo 2

Vamos começar fazendo um esboço do nosso triângulo

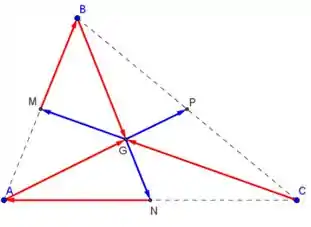
Do desenho, podemos dizer que:

M A → + A G → = G M → B G → + N G → = G N → C G → + P C → = G P →

E pelo esboço da definição dado na questão 4-13, temos:

2 M A → = 2 G M → - 2 A G → 2 N B → = 2 G N → - 2 B G → 2 P C → = 2 G P → - 2 C G →

Passo 3

Vamos expandir a soma encontrada, obtendo:

M N → + N B → + A D → + M A → = A B → - D C →

M N → + N B → + M D → = A B → - D C →

M N → + N B → + M D → + D N → - D N → = A B → - D C →

M N → = 1 2 A B → - D C →

Passo 4

Somando as equações, temos:

B A + A C + C B = 2 1 3 C G → + 1 3 A G → + 1 3 B G → - 2 A G → + B G → + C G → =

= - 2 3 C G → + A G → + B G →

C G → + A G → + B G → = 0

Pronto! Portanto, temos que o baricentro do triângulo ABC também é o baricentro dos pontos de seus vértices. 😉

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se os pontos A e B são equidistantes da origem e os segmentos orientados OA e BC são equipolentes, prove que OC e AB são perpendiculares.
Seja AA′ uma diagonal de um cubo e sejam B, C e D os vértices desse cubo que estão mais próximos de A. Mostre que AA′ é perpendicular a BC e BD e conclua que AA′ é perpendicular ao plano BCD. Mostre a
Ache quatro pontos A, B, C e D no espaço, cujas coordenadas sejam 1 ou 0, de modo que ABCD seja um tetraedro regular. Verifique que duas arestas opostas desse tetraedro são ortogonais.
Dados os pontos distintos A = (a, b, c), A ′ = (a ′, b′, c′) e o número d0, mostre que existem, na reta AA′, 0, 1 ou 2 pontos P tais que d (O, P) = d. Se existir exatamente um ponto P com d (O, P) = d
Dado um triângulo acutângulo A B C , mostre que existe um ponto O no espaço, tal que os Ângulos A Ô B ,A Ô CeB Ô C Ô Ô Ô são retos. Determine as medidas das arestas e da altura da pirâmide de base A B